Definizione-Proposizione 1 Sia

un gruppo e sia $\mathcal{R}$ una relazione di equivalenza su

, compatibile con il prodotto di

, cioè tale che, se $a\mathcal{R} a'$ e $b\mathcal{R} b'$ , allora $aa'\mathcal{R} bb'$ .
L'insieme delle classi di equivalenza di $\mathcal{R}$ , con il prodotto definito da

$\begin{displaymath}[a]\cdot[b] = [a b],\end{displaymath}$

è un gruppo, detto gruppo quoziente, e denotato con $G/\mathcal{R}$ . L'elemento neutro di $G/\mathcal{R}$ è

, e per ogni $[a]\in G/\mathcal{R}$ l'inverso di

è $[a^{-1}]$ .
Se

è abeliano, anche $G/\mathcal{R}$ lo è.

Dimostrazione
Il prodotto $\cdot$ di $G/\mathcal{R}$ è ben definito essendo $\mathcal{R}$ compatibile con il prodotto di , ed è associativo in quanto

$\begin{displaymath}[a]\cdot([b]\cdot [c]) = [a]\cdot [b c] = [a(bc)] = [(a b) c] = [ab]\cdot [c] = ([a]\cdot [b])\cdot [c],\end{displaymath}$

$\forall [a] , [b] , [c] \in G/\mathcal{R}.$ Inoltre si ha:

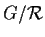$[a]\cdot [1] = [a1] = [a]$ e $[1]\cdot [a] = [1a] = [a]$ , $\forall [a] \in G/\mathcal{R}$ , cioè è l'elemento neutro di $G/\mathcal{R}$ ;
$[a]\cdot[a^{-1}] = [a a^{-1}] = [1]$ e $[a^{-1}]\cdot [a] = [a^{-1} a] = [1]$ , $\forall [a] \in G/\mathcal{R}$ , cioè $[a^{-1}]$ è l'inverso di .