Esempio 5
Consideriamo il gruppo degli interi
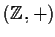
.
I
sottogruppi di
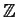
sono tutti della forma
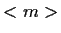
,
con
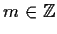
,
e sono tutti normali essendo
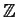
abeliano.
Anziché scrivere
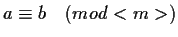
,
si scrive
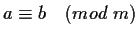
.
Se
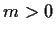
,
il gruppo quoziente
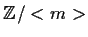
è
abeliano, essendo
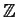
abeliano, ha ordine
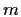
e i suoi elementi sono
![$[0],\ldots,[m-1]$](img10.gif)
.
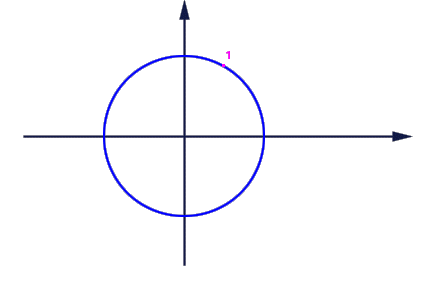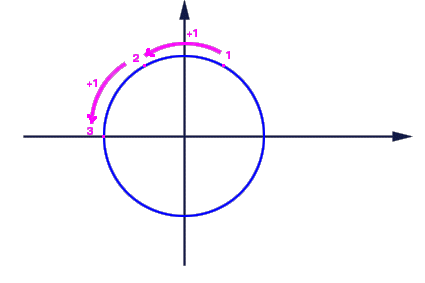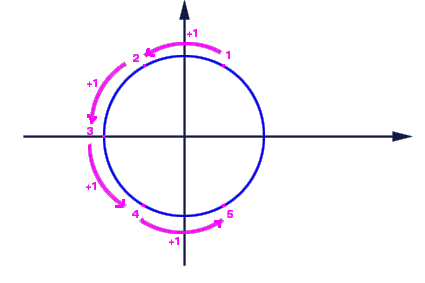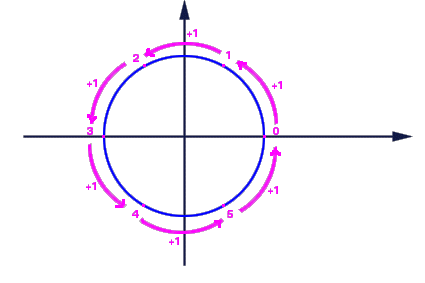
Infatti dato un intero
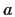 ,
se si divide
,
se si divide 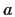 per
per 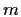 ,
si ottiene:
,
si ottiene:
Questo equivale a dire
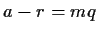
,
cioè
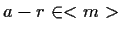
,
e quindi
Allora
![$a\in [r]$](img16.gif)
.
Inoltre gli elementi
![$[0],\ldots,[m-1]$](img10.gif)
sono distinti in quanto se
![$[a]=[b] $](img17.gif)
,
con
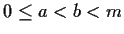
,
si ha
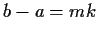
e
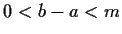
,
quindi
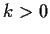
e
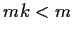
che
è assurdo.
Il gruppo
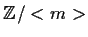
viene indicato con
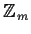
e si chiama il
gruppo degli interi modulo
m.

![]() ,
se si divide
,
se si divide ![]() per
per ![]() ,
si ottiene:
,
si ottiene: 
![]() ,
se si divide
,
se si divide ![]() per
per ![]() ,
si ottiene:
,
si ottiene: