Esempio 6   Facendo ancora riferimento alle notazioni dell'esempio 5 della sezione "Gruppi: definizione e prime proprietà", sia $H=<\sigma_{1}>$ in $S_{3}$. Per ogni $\alpha,\beta \in S_{3}$, $\alpha \equiv_{H}\,\beta$ se e solo se $\alpha \beta^{-1}\in H$, cioè se e solo se $\alpha\beta^{-1}=id$ o $\alpha\beta^{-1}=\sigma_{1}$ che equivale a dire $\alpha=\beta$ o $\alpha\beta^{-1}=\sigma_{1}$, cioè $\alpha=\sigma_{1}\beta$.

Esempio 7   Sia $H = < m >=\{km\vert\; k\in \mathbb{Z}\}$ un sottogruppo di $\mathbb{Z} $. Per ogni $a , b \in \mathbb{Z} $, $a\;\equiv_{H}\; b$ se $a - b = km$ per un certo $k \in \mathbb{Z} $.
In questo caso si dice anche che $a , b$ sono congrui modulo $m$.

Proposizione 8   Sia $G$ un gruppo e sia $a\in G$.
Allora $Ha = \{x\in G \vert\, a \equiv_{H}\,x\}$, cioè il laterale destro $Ha$ coincide con la classe di equivalenza di $a$ rispetto a $\equiv_{H}$.

Dimostrazione
Poniamo $[a]=\{x\in G\vert\, a\equiv_{H}\,x\}$.
Sia $ha$ un elemento di $Ha$.
Si ha: $a(ha)^{-1} = aa^{-1} h^{-1}= h^{-1} \in H $, cioè $ha \equiv_{H} \, a$ e quindi $ha \in [a]$; allora $Ha \subseteq [a]$.
Sia ora $x$ un elemento di $[a]$.
Si ha: $x\equiv_{H}\, a$, cioè $xa^{-1}\in H $ che è equivalente a $xa^{-1} = h$ per un certo $h \in H$. Allora $x = ha $ cioè $x\in Ha$ e quindi $[a]\subseteq Ha$.

Corollario 9   Se $G$ è un gruppo e $H$ un suo sottogruppo, due laterali destri di $H$ in $G$ o coincidono o non hanno elementi in comune.

Dimostrazione
L'affermazione segue dal fatto che i laterali destri, come visto in proposizione 8, sono classi di equivalenza, che quindi ripartiscono $G$ in sottoinsiemi disgiunti.

Proposizione 10   Sia $G$ un gruppo e sia $H$ un sottogruppo di $G$.
Due qualsiasi laterali destri di $H$ in $G$ hanno la stessa cardinalità.

Dimostrazione
Siano $Hx$ e $Hy$ due laterali destri di $H$ in $G$ e sia $f$ l'applicazione

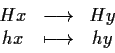
\begin{displaymath}\begin{array}{ccc} Hx &\longrightarrow &Hy \\ hx & \longmapsto & hy\end{array}\end{displaymath}

Proviamo che tale applicazione è biunivoca; $f$ è suriettiva ed è iniettiva in quanto se $f(h_{1} x) = f(h_{2} x)$, allora $h_{1} y = h_{2} y$, cioè $h_{1} = h_{2} $ per la legge di cancellazione in $G$, e quindi $h_{1}x = h_{2}x$.

Corollario 11   Sia $G$ un gruppo e sia $H$ un suo sottogruppo.
Allora la cardinalità di $Ha$ è uguale alla cardinalità di $H$, $ \forall a \in G$.

Dimostrazione
L'affermazione segue dalla proposizione 10, osservando che $H = H1$.

previousup next esercizi