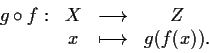
Sia ora
con l'operazione di composizione è un gruppo. Infatti :
- la composizione è associativa:
notiamo dapprima che le scritture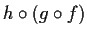 e
e
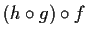 hanno senso; inoltre
hanno senso; inoltre
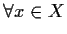 ,
,
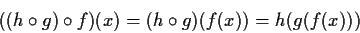
e
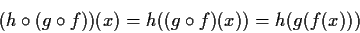
cioè
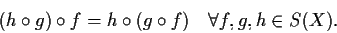
- la funzione identità su
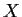 ,
,
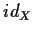 ,
è
l'elemento neutro di
,
è
l'elemento neutro di 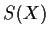 :
:
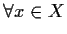 ,
,
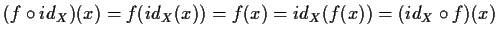 ,
,
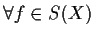 ;
;
- per ogni
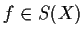 ,
l'applicazione inversa di
,
l'applicazione inversa di 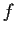 ,
,
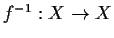 ,
è l'inverso di
,
è l'inverso di 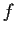 in
in 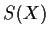 :
:
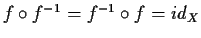 .
.
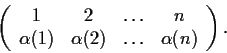
La composizione di due permutazioni di
Per esempio, se
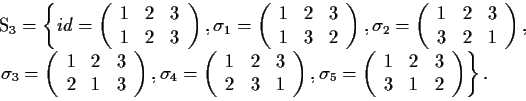
La tavola di moltiplicazione di
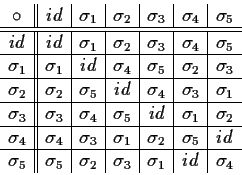
Esempio 6 Sia
- la composizione è un'operazione binaria su
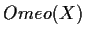 ,
ed
è associativa;
,
ed
è associativa;
-
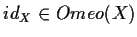 ;
;
-
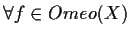 ,
,
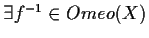 .
.
Proposizione 7
Se ![]() e
e ![]() sono due gruppi, con elementi neutri rispettivamente
sono due gruppi, con elementi neutri rispettivamente
![]() e
e ![]() ,
il prodotto
,
il prodotto
![]() è un gruppo con la seguente
operazione:
è un gruppo con la seguente
operazione:
L'elemento neutro è
Dimostrazione
- L'associatività del prodotto segue dall'associatività
delle due operazioni di
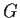 e
e 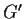 ;
;
- per ogni
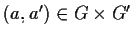 ,
,
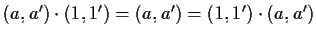 ;
;
- per ogni
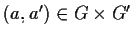 ,
,
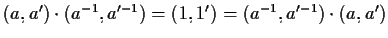 .
.
