Osservazione 8
Se
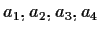 sono quattro elementi di
un gruppo
sono quattro elementi di
un gruppo 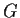 ,
ci sono vari modi di moltiplicarli tra loro,
conservando l'ordine; si hanno infatti le seguenti
possibilità:
,
ci sono vari modi di moltiplicarli tra loro,
conservando l'ordine; si hanno infatti le seguenti
possibilità:
La proposizione seguente mostra che tali prodotti
hanno tutti lo stesso valore.
Proposizione 9
In un gruppo
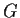
vale l'associativa generalizzata, cioè dati
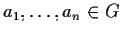
,
con
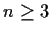
,
il loro
prodotto, eseguito disponendo in modo qualunque le parentesi, dà
un risultato che dipende solo da
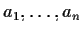
e che
quindi
può essere denotato con
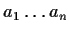
omettendo le
parentesi.
La scrittura
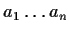
indica quindi che
gli
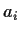
vanno moltiplicati nell'ordine assegnato, associandoli
però come si vuole.
Dimostrazione
Procediamo per induzione su
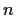
.
Se
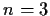
l'affermazione è la
proprietà associativa del prodotto.
Supponiamo ora vera
l'affermazione per ogni
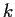
compreso tra
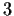
e
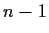
e proviamola per
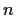
.
Indichiamo con
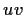
e
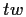
due diversi prodotti di
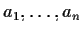
, essendo
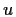
e
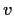
prodotti in cui
compaiono
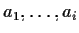
e
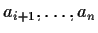
rispettivamente e
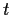
e
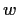
prodotti in cui compaiono
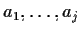
e
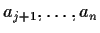
rispettivamente, con
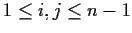
.
I prodotti
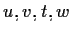
sono eseguiti
disponendo in un certo modo le parentesi; ad esempio:
Se
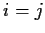
,
per l'ipotesi
induttiva, si ha:
e quindi
Se invece
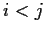
,
ancora per l'ipotesi
induttiva, si ha:
e
da cui segue:
In ogni caso quindi
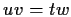
,
cioè il prodotto di
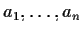
non dipende da come vengono associati
gli
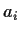
.
![]() sono quattro elementi di
un gruppo
sono quattro elementi di
un gruppo ![]() ,
ci sono vari modi di moltiplicarli tra loro,
conservando l'ordine; si hanno infatti le seguenti
possibilità:
,
ci sono vari modi di moltiplicarli tra loro,
conservando l'ordine; si hanno infatti le seguenti
possibilità: 