Definizione 11   Sia $(G,\cdot)$ un gruppo e sia $a$ un elemento di $G$.
Se $n\in \mathbb{Z} $, la potenza n-esima di $a$, denotata con $a^{n}$, è definita come:

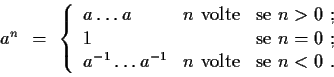
\begin{eqnarraystar}\mbox{$a^{n}$ }& = & \left \{\begin{array}{lcc} a\ldots a ... ...ox{$n$\space volte} & \mbox{se $n < 0$ .} \end {array}\right.\end{eqnarraystar}



Se stiamo usando per $G$ la notazione additiva, definiamo invece il prodotto di un intero $n$ per un elemento $a\in G$ come:

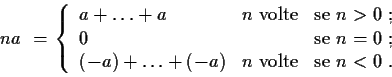
\begin{eqnarraystar}\mbox{$na$ } &=& \left\{ \begin {array}{lcc} a+\ldots+a &\... ...mbox{$n$\space volte} &\mbox{se $n < 0$ .} \end{array}\right.\end{eqnarraystar}

Osservazione 12   Dalla definizione 11 seguono le seguenti proprietà:
1)
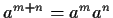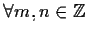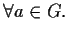
$a^{m+n}= a^{m} a^{n}$,      $\forall m,n\in\mathbb{Z} $ e $\forall a\in G.$
2)
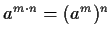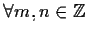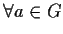$a^{m\cdot n}= (a^{m})^{n}$,     $\forall m,n\in\mathbb{Z} $ e $\forall a\in G$.
3)
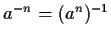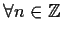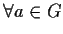$a^{-n}= (a^{n})^{-1}$,     $\forall n\in\mathbb{Z} $ e $\forall a\in G$.
4)
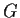Se $G$ è abeliano:
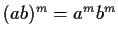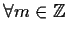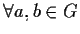$(a b)^{m} = a^{m} b^{m}$,     $\forall m\in \mathbb{Z} $ e $\forall a,b\in G$.
Tali proprietà, ora scritte in notazione moltiplicativa, in un gruppo additivo diventano:
1)
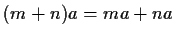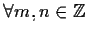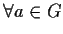$(m + n) a = ma + na$,     $\forall m,n\in\mathbb{Z} $ e $\forall a\in G$.
2)
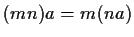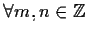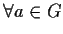$(mn) a = m (na)$,     $\forall m,n\in\mathbb{Z} $ e $\forall a\in G$.
3)
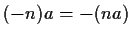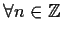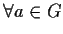$(-n) a = -(na)$,     $\forall n\in\mathbb{Z} $ e $\forall a\in G$.
4)
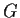Se $G$ è un gruppo abeliano:
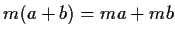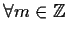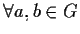$m (a + b) = ma + mb$,     $\forall m\in \mathbb{Z} $ e $\forall a,b\in G$.


previousup next esercizi