Osservazione 2   Se $(G,*)$ è un gruppo, allora:

1)
l'elemento neutro è unico.
Infatti se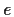 $e$ e $e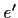'$ sono elementi neutri, si ha :
$e = e*e' = e'$.
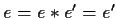2)
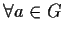$\forall a \in G$, esiste un unico inverso $a'$.
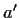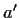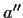Infatti se $a'$ e $a''$ sono inversi di 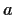$a$, si ha:
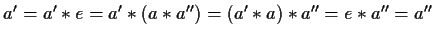$a' = a'*e = a'*(a*a'') = (a'*a)*a'' = e*a''= a''$.

Notazione 3   L'operazione $*$ definita nell'insieme $G$ si indica quasi sempre con $+$ o con $\cdot $.
Nel primo caso si parla di gruppo additivo, l'elemento neutro viene indicato con $0$ e per ogni $a\in G$, l'inverso $a'$ viene chiamato opposto ed è indicato con $-a$.
Nel secondo caso invece si parla di gruppo moltiplicativo, l'elemento neutro viene denotato con $1$ e per ogni $a\in G$l'inverso di $a$ è indicato con $a^{-1}$.
Scriveremo più brevemente ``gruppo $G$'' invece di ``gruppo $(G,*)$''.
La notazione usata quasi sempre sarà quella moltiplicativa.
Indicheremo inoltre il prodotto di due elementi $a,b$ di $G$, con $a\cdot b$ o $ab$.

Esempi 4  
1)
$(\mathbb{N} ,+)$, $(\mathbb{N} ,\cdot )$ non sono gruppi: non per tutti gli $n\in\mathbb{N} $ esiste l'inverso.
2)
$(\mathbb{Z} ,+) $ è un gruppo il cui elemento neutro è lo $0$.
$(\mathbb{Z} ,\cdot)$ non è invece un gruppo.
3)
$(\mathbb{Q} ,+)$, $(\mathbb{R} ,+)$, $(\mathbb{C} ,+)$, $(\mathbb{Q} ^{*},\cdot)$, $(\mathbb{R} ^{*},\cdot)$ sono gruppi commutativi.
4)
L'insieme $\mathbb{C^{*}} $ dei numeri complessi non nulli

\begin{displaymath}\{a+ib\vert a,b\in \mathbb{R} , \mbox{non entrambi nulli}\},\end{displaymath}

con il prodotto definito da $(a+ib)\cdot(c+id)=(ac-bd)+i(ad+bc)$, è un gruppo il cui elemento neutro è $1=1+i0$.
Infatti:
  • il prodotto è associativo:
    $(a+ib)\cdot[(c+id)\cdot(e+if)]=(a+ib)\cdot[(ce-df)+i(cf+de)]=$
    $=(a(ce-df)-b(cf+de))+i(a(cf+de)+b(ce-df))$
    e
    $[(a+ib)\cdot(c+id)]\cdot (e+if)=[(ac-bd)+i(ad+bc)]\cdot(e+if)=$
    $=((ac-bd)e-(ad+bc)f)+i((ac-bd)f+(ad+bc)e)=$
    $=(a(ce-df)-b(de+cf))+i(a(cf+de)+b(ce-df)),$
    cioè $(a+ib)\cdot[(c+id)\cdot(e+if)]=[(a+ib)\cdot(c+id)]\cdot(e+if);$
  • $1+i0$ è l'elemento neutro:
    $(a+ib)\cdot(1+i0)=(a\cdot 1-b\cdot 0)+i(a\cdot 0+b\cdot 1)=a+ib$ e in modo analogo si vede $(1+i0)\cdot (a+ib)=(a+ib)$;
  • $\forall a+ib\in \mathbb{C^{*}} $, $(a+ib)^{-1}=\frac{a}{a^{2}+b^{2}}-i\frac{b}{a^{2}+b^{2}}\in \mathbb{C^{*}} .$

previous up next esercizi