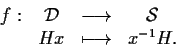Osservazione 12
I risultati ottenuti per i laterali destri, si possono trovare in
modo del tutto analogo anche per i laterali sinistri, sostituendo
la relazione
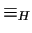
,
con la relazione su
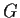
definita da:
Precisamente,
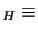
è una
relazione di equivalenza su
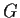
,
le cui classi di equivalenza sono i
laterali sinistri di
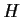
:
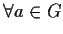
,
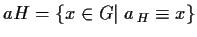
.
Inoltre
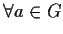
,
la cardinalità di
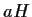
è
uguale alla cardinalità di
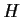
;
dunque,
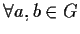
,
la cardinalità di
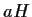
è uguale alla
cardinalità di
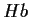
.
Proposizione 13
Sia
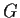
un gruppo e sia
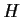
un suo sottogruppo.
Esiste una corrispondenza biunivoca tra l'insieme dei laterali destri
di
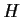
in
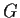
e l'insieme dei laterali sinistri di
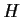
in
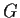
.
Dimostrazione
Sia
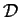
l'insieme dei laterali destri di
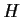
in
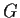
,
e
sia
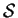
l'insieme dei laterali sinistri di
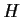
in
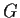
.
Consideriamo l'applicazione
Innanzitutto proviamo che
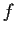
è ben definita, cioè
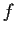
non
dipende dalla scelta del rappresentante del laterale destro; sia
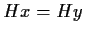
,
allora
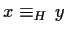
,
cioè
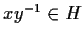
.
Allora
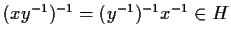
.
Questo equivale a
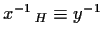
cioè
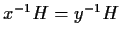
e
quindi
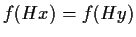
.
Inoltre
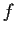
è suriettiva ed è iniettiva in quanto se
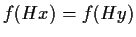
,
allora
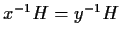
da cui segue che
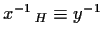
,
cioè
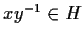
,
che implica
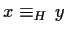
,
cioè
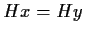
.