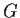
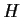
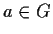
Definizione 1   Sia $G$ un gruppo e sia $H$ un suo sottogruppo. Se $a\in G$, l'insieme

\begin{displaymath}Ha := \{ha , h\in H\}\end{displaymath}

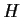
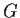
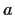
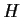
è detto laterale destro di $H$ in $G$ (o, se si preferisce specificare, ``il laterale destro di $a$ relativo ad $H$ in $G$'').
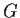
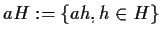
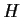
Analogamente $aH := \{ah , h\in H\}$ è detto laterale sinistro di $H$ in $G$.

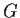
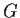
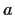
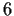
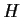
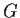
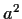
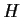
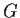
Esempio 2   Sia $G$ un gruppo ciclico generato da $a$, di ordine $6$; sia $H$ il sottogruppo di $G$ generato da $a^{2}$. I laterali destri di $H$ in $G$, sono:

\begin{displaymath}H (= H1 = Ha^{2}= Ha^{4})\;\mbox{e}\;Ha = \{ a,a^{3},a^{5}\}(= Ha^{3} = Ha^{5}).\end{displaymath}

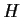
Questi sono anche i laterali sinistri di $H$ in $G$.

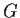
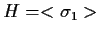
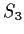
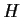
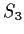
Esempio 3   Facendo riferimento alle notazioni dell'esempio 5 della sezione "Gruppi: definizione e prime proprietà", sia $H=<\sigma_{1}>$ in $S_{3}$. I laterali destri di $H$ in $S_{3}$ sono

\begin{displaymath}H(=Hid=H\sigma_{1}),\; H\sigma_{2}=\{\sigma_{2},\sigma_{4}\}(... ...ma_{4}),\; H\sigma_{3}=\{\sigma_{3},\sigma_{5}\}(=H\sigma_{5}).\end{displaymath}

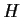
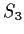
I laterali sinistri di $H$ in $S_{3}$ sono invece

\begin{displaymath}H(=idH=\sigma_{1}H),\; \sigma_{2}H=\{\sigma_{2},\sigma_{5}\}... ...a_{5}H),\; \sigma_{3}H=\{\sigma_{3},\sigma_{4}\}(=\sigma_{4}H).\end{displaymath}

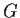
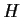
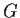
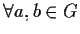
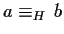
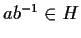
Definizione 4   Sia $G$ un gruppo e sia $H$ un suo sottogruppo. Definiamo su $G$ la seguente relazione: $\forall a,b\in G$, $a\equiv_{H} \,b$, se e solo se $ab^{-1}\in H$.

Proposizione 5   La relazione $\equiv_{H}$ è una relazione di equivalenza su $G$.

Dimostrazione
La relazione è infatti:

previousup next esercizi