Notazione 1
Sia
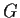
un gruppo, sia
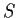
un suo sottoinsieme, e sia
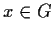
.
Si pone:
analogamente
a quanto fatto in
definizione 1 della sezione "Laterali di un sottogruppo". Quindi
Se
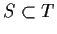
e
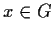
,
si ha
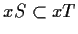
e
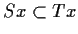
.
Proposizione 3
Sia
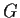
un gruppo e sia
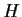
un suo sottogruppo. Allora sono equivalenti:
- 1)
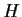 è normale.
è normale.
- 2)
-
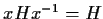 ,
,
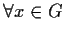 .
.
- 3)
- Ogni laterale destro di
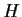 è anche laterale
sinistro.
è anche laterale
sinistro.
- 4)
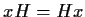 ,
,
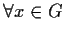 .
.
- 5)
- Le relazioni
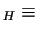 e
e
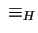 coincidono.
coincidono.
Se queste condizioni equivalenti sono verificate, la relazione di
equivalenza
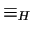
verrà detta congruenza modulo
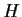
,
e
scriveremo
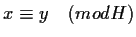
.
Chiameremo ``
laterale di
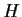
'' ogni suo laterale sia destro che sinistro
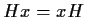
.
Dimostrazione
-
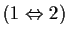
- Se
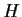 è normale, si ha:
è normale, si ha:
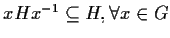 .
.
Quindi vale
cioè
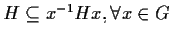 .
Questo è
equivalente a
.
Questo è
equivalente a
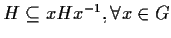 .
.
La
doppia inclusione dà quindi
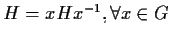 .
.
Viceversa se
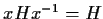 ,
,
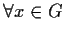 ,
,
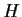 è
ovviamente normale.
è
ovviamente normale.
-
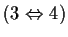
- Se un
laterale destro di
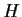 ,
,
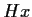 ,
è uguale ad un laterale
sinistro, necessariamente tale laterale è
,
è uguale ad un laterale
sinistro, necessariamente tale laterale è 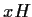 ,
cioè
,
cioè 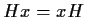 .
Infatti, poiché
.
Infatti, poiché 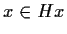 ,
,
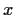 deve stare anche nel
laterale sinistro cercato. D'altra parte
deve stare anche nel
laterale sinistro cercato. D'altra parte 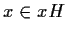 ,
ed essendo i
laterali sinistri disgiunti, il laterale sinistro cercato è
necessariamente
,
ed essendo i
laterali sinistri disgiunti, il laterale sinistro cercato è
necessariamente 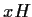 .
.
-
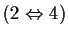
- Si ha:
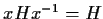 ,
,
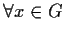 se e solo se
se e solo se
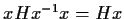 ,
,
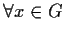 ,
cioè se e solo
se
,
cioè se e solo
se 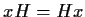 ,
,
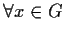 .
.
-
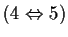
- Le relazioni
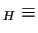 e
e
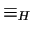 coincidono, se e
solo se le rispettive classi di equivalenza di ogni
coincidono, se e
solo se le rispettive classi di equivalenza di ogni 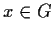 coincidono,
cioè
coincidono,
cioè
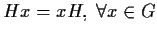 .
.