- 1)
- Se
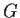 è abeliano ogni sottogruppo
è abeliano ogni sottogruppo 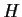 di
di 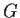 è
normale.
è
normale.
- 2)
- Se
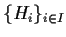 è una famiglia
di
sottogruppi
normali di
è una famiglia
di
sottogruppi
normali di 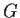 ,
anche il sottogruppo
,
anche il sottogruppo
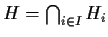 è normale.
è normale.
- 1)
- Se
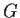 è abeliano,
è abeliano, 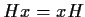 ,
,
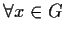 ,
allora per proposizione 3,
,
allora per proposizione 3, 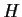 è normale.
è normale.
- 2)
- Poiché
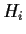 è normale per tutti
gli
è normale per tutti
gli 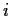 ,
,
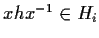 ,
,
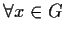 ,
,
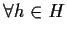 e
e
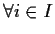 .
Allora
.
Allora
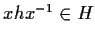 ,
,
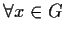 e
e
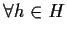 ,
cioè
,
cioè 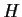 è normale.
è normale.
