Chiamiamo invece, centralizzante di
In particolare :
- se
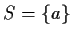 ,
normalizzante e centralizzante di
,
normalizzante e centralizzante di 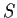 coincidono, e corrispondono all'insieme degli elementi di
coincidono, e corrispondono all'insieme degli elementi di 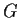 che
commutano con
che
commutano con 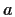 :
:
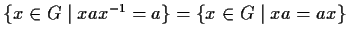 .
Tale insieme viene anche denotato con
.
Tale insieme viene anche denotato con
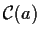 ;
;
- se
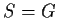 ,
il centralizzante di
,
il centralizzante di 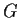 viene chiamato
centro di
viene chiamato
centro di 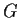 ,
ed è l'insieme degli elementi di
,
ed è l'insieme degli elementi di 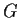 che
commutano con tutti gli altri.
che
commutano con tutti gli altri.
Osservazione 7
Si verifica facilmente che sia ![]() che
che ![]() sono
sottogruppi di
sono
sottogruppi di ![]() ,
e che
il centro di
,
e che
il centro di ![]() è un sottogruppo normale di
è un sottogruppo normale di ![]() stesso.
stesso.
Inoltre se
![]() è un sottogruppo di
è un sottogruppo di ![]() ,
si ha:
,
si ha:
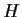 è normale in
è normale in 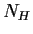 ;
;
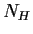 è il più grande sottogruppo di
è il più grande sottogruppo di 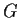 in cui
in cui 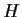 è
normale;
è
normale;
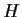 è normale in
è normale in 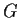 se e solo se
se e solo se 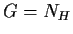 .
.
