Bolyai e Lobachevsky


Nicolai Lobachevsky	Jànos Bolyai

    Dopo un iniziale tentativo di dimostrare il quinto postulato, Gauss (1777-1855) arrivò gradualmente alla convinzione che esisteva una geometria che in sè non ha nulla di contraddittorio. Ma, a causa della discrezione con cui Gauss mosse questi primi passi, tutto l'onore della scoperta fu tributato poco dopo a due matematici più giovani che, all'insaputa uno dell'altro ed in lontani paesi, giunsero quasi contemporaneamente ad analoghi risultati: l' ungherese Jànos Bolyai (1802-1860) ed il russo Nicolai Ivanovich Lobachevsky (1793-1856).

    Essi pubblicarono delle presentazioni organiche di una geometria non euclidea su basi deduttive sintetiche rendendoso pienamente conto che questa nuova geometria era dal punto di vista logico altrettanto legittima quanto quella di Euclide.     Nicolai Ivanovich Lobachevsky studiò all'Università di Kazan di cui fu professore e rettore dal 1827 al 1846. Espose le sue vedute sui fondamenti della geometria in un lavoro letto di fronte al dipartimento di Matematica e Fisica dell'Università nel 1826. Tuttavia, il lavoro non fu mai stampato e andò perduto. In seguito espose il suo approccio alla Geometria non Euclidea in una serie di lavori, i primi due dei quali furono pubblicati in riviste di Kazan e il terzo nel "Journal fur Mathematik".
    Il primo era intitolato Sui fondamenti della geometria e apparve nel 1829-30. Il secondo, intitolato Nuovi fondamenti della geometria con una teoria completa delle parallele (1835-37) era una presentazione migliore delle idee di Lobachevsky. Egli chiamava la sua nuova geometria "geometria immaginaria" per motivi che sono forse già chiari e che lo diventeranno di più in seguito.
    Le prime pubblicazioni di Lobachevsky sulla Geometria non Euclidea erano scritte in Russo, quindi il suo lavoro non diventò subito noto nell'Europa centrale e occidentale, fino ad alcuni anni dopo, quando cominciò a pubblicare degli appunti in Francese (1837) e Tedesco (1840). Pur essendo diventato cieco, dettò un'esposizione completamente nuova della sua geometria e la pubblicò nel 1855 con il titolo Pangéométrie.
    Jànos Bolyai, figlio di Wolfgang Farkas Bolyai (1775-1856), era un ufficiale ungherese. Sulla Geometria non Euclidea, che chiamava Geometria Assoluta, scrisse un lavoro di ventisei pagine intitolato La scienza dello spazio assoluto , che fu pubblicato in appendice al libro del padre intitolato Tentamen Juventutem Studiosam in Elementa Matheseos. Anche se quest'opera in due volumi apparve nel 1832-33, e quindi dopo il primo lavoro di Lobachevsky, sembra che Bolyai abbia elaborato le sue idee sulla Geometria non Euclidea prima del 1825 e che entro quel periodo si fosse convinto che la nuova geometria non era contraddittoria. In una lettera al padre datata 23 Novembre 1823 Jànos scrive: "Ho fatto delle scoperte così meravigliose che sono io stesso sconvolto per lo stupore".
    Le ricerche di Bolyai erano così simili a quelle di Lobachevsky che quando Bolyai vide per la prima volta nel 1835 i lavori del russo pensò che li avesse copiati dalla sua pubblicazione del 1832-33.
    Gauss lesse l'articolo di Jànos Bolyai nel 1832 e scrisse a Farkas che non poteva lodarlo perché, così facendo, avrebbe lodato le proprie ricerche.Il procedimento seguito (separatamente) dai due matematici è il seguente:

Dati una retta AB e un punto P complanare ed esterno ad essa, sia PO la perpendicolare alla retta passante per il punto P .
Si consideri ora un punto D sulla retta AB ; per esso passerà la retta PD secante la retta data.
Si faccia muovere il punto D nel verso OB : in corrispondenza di ogni posizione occupata da D sulla retta, si otterrà una secante PD alla retta assegnata.
Si consideri ora la distanza OD tendente all'infinito; troveremo in corrispondenza una retta PL che non intersecherà la retta AB , e che quindi sarà parallela ad OB.

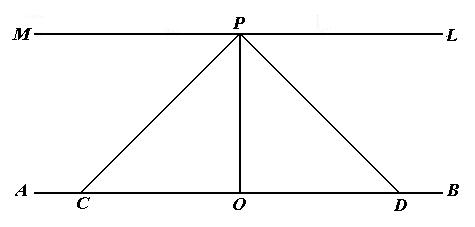
Figura 11. "situazione euclidea"

Si proceda in ugual modo dall'altra banda; anche in questo caso si troverà una retta PM non secante la retta data, e pertanto parallela ad OA. Ora, secondo la Geometria Euclidea, PL e PM formano un'unica retta parallela ad AB, e gli angoli OPL e OPM sono uguali e retti.
Si assuma invece l'ipotesi dell'angolo acuto, allora PL e PM saranno due rette distinte, ed entrambe parallele ad AB pur senza essere equidistanti in ogni punto rispetto alla retta data. PL è parallela ad OB e PM è parallela ad OA , inoltre ognuna di esse, pur prolungata all'infinito nel verso del parallelismo, non incontrerà mai la retta data, e la distanza da questa diminuirà infinatamente.

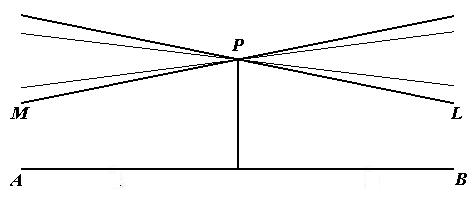
Figura 12. "situazione non euclidea"

Avremo inoltre che (vedi figura 12), tutte le rette fra PL e PM sono parallele ad AB .

pagina precedente torna all'indice pagina successiva