LE CURVE NELL´ANTICA GRECIA
Gli antichi greci si chiesero prima di tutto quali strumenti si potessero usare nella risoluzione di problemi geometrici e la risposta che si diedero fu semplice: potevano essere usati solamente un compasso e una riga non graduata. Tutto ciò che era possibile tracciare con la combinazione di questi due strumenti era leggittimato. Il senso di questa "autolimitazione" sta soprattutto nel fatto che le costruzioni geometriche dovevano essere abbastanza semplicemente eseguibili e disegnabili, perché esse costituivano allora un vero e proprio "strumento di calcolo": arrivare con una costruzione geometrica a disegnare un segmento che rappresentasse una grandezza che si voleva determinare costituiva (misurando poi il segmento disegnato) un metodo di determinazione di quella grandezza, proprio come un ingegnere usava (fino agli anni '60) un regolo calcolatore, ed oggi usa le calcolatrici.
Ben presto i geometri greci si imbatterono in tre problemi che misero a dura prova queste semplici regole stabilite: la quadratura del cerchio, la duplicazione del cubo e la trisezione dell’angolo. Questi tre problemi avevano la caratteristica di essere irrisolvibili con solo riga e compasso, ma soprattutto non era facile accorgersi del fatto che fossero irrisolvibili; infatti solo nel XIX° secolo i matematici dimostrarono con strumenti algebrici che con il solo utilizzo di riga e compasso i tre problemi non erano determinabili.
Il primo problema, quello della quadratura del cerchio, chiedeva di determinare un quadrato avente la stessa area di un cerchio dato. Tale problema venne esteso successivamente alla quadratura di altre figure piane: alcune avevano una soluzione facile, altre difficile; per il cerchio la soluzione era impossibile. Il primo a studiare il problema fu Ippocrate di Chio (da non confondere con il famoso medico) che giunse alla quadratura molte figure tra cui le lunule. Successivamente Ippia scoprì una curva (non costruibile con solo riga e compasso), detta appunto quadratrice, che permetteva di risolvere il problema; probabilmente fu Dinostrato a intuire che la curva avesse la suddetta proprietà.
Archimede si cimentò nella quadratura della circonferenza utilizzando la sua spirale ed inoltre quadrò molte curve e figure geometriche; ricordiamo la famosa quadratura della parbola.
In epoca moderna molti matematici si cimentarono con questo problema e trovarono soluzioni (ovviamente non con il solo ausilio di riga e compasso). Soltanto nel 1882 von Lindenmann dimostrò rigorosamente con strumenti algebrici l´impossibilità del problema (di fatto egli si accorse che il rapporto tra circonferenza e diametro era un numero trascendente).
Il secondo problema era la trisezione dell´angolo. Per risolverlo bisognava costruire un angolo di ampiezza un terzo rispetto ad un qualsiasi angolo dato (ovviamente alcuni angoli erano facilmente trisecabili). Il problema nacque dalla semplicità con il quale gli antichi greci risolsero il problema di dividere in due parti uguali un angolo di dimensioni qualsiasi. Essi pensarono dunque che anche trisecarlo doveva essere semplice, ma non era così. Per risolvere il problema Nicomede uitlizzò la concoide, Archimede la sua spirale e Pappo le coniche riprendendo un idea di Apollonio. Nel rinascimento Pascal risolse il problema con una curva chiamata lumaca (di Pascal) e più tardi Mac Laurin con una curva chiamata appunto trisettrice. Solo nel 1837 Wantzel, con metodi algebrici, dimostrò che il problema era insolubile con il solo utilizzo di riga e compasso.
Il terzo problema, infine, quello della duplicazione del cubo, chiedeva di torvare un cubo
di lato 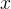 tale che il suo volume fosse il doppio del volume di un cubo con lato
assegnato. In termini algebrici bisognava trovare
tale che il suo volume fosse il doppio del volume di un cubo con lato
assegnato. In termini algebrici bisognava trovare 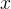 tale che
tale che
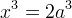 con
con 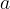 dato. Il problema viene anche
detto "problema di Delo", perchè secondo il mito gli ateniesi si rivolsero all´
oracolo di Delo per contrastare un´epidemia. L´oracolo rispose che per placare l´ira degli dei avrebbero dovuto
costruire un altare doppio rispetto a quello esistente. Gli ateniesi obbedirono, ma non vedendo scomparire l´epidemia si
rivolsero di nuovo all´oracolo il quale disse loro che l´altare era otto volte più grande poichè lo
avevano costruito con uno spigolo doppio.
dato. Il problema viene anche
detto "problema di Delo", perchè secondo il mito gli ateniesi si rivolsero all´
oracolo di Delo per contrastare un´epidemia. L´oracolo rispose che per placare l´ira degli dei avrebbero dovuto
costruire un altare doppio rispetto a quello esistente. Gli ateniesi obbedirono, ma non vedendo scomparire l´epidemia si
rivolsero di nuovo all´oracolo il quale disse loro che l´altare era otto volte più grande poichè lo
avevano costruito con uno spigolo doppio.
Menecmo utilizzò le coniche per risolvere il problema; Diocle la sua cissoide. Una soluzione è attribuita addirittura a Platone il quale sembra abbia utilizzato un metodo chiamato neusis che consisteva nello scorrimento e rotazione di aste graduate, fino a soddisfare le condizioni richieste.
I procedimenti algebrici utilizzati da Wantzel per dimostrare l´impossibilità di trovare una soluzione al problema precedente sono utili allo stesso modo per dimostrare anche l´impossibilità di duplicare un cubo con i soli riga e compasso.