LA CONCOIDE DI NICOMEDE

 

 

Storia

La concoide (o clocoide) di Nicomede prende il nome dall´omonimo matematico e filosofo vissuto a cavallo tra il III° e il II° sec. a.C. ad Alessandria ed Atene. Queste poche notizie sono giunte a noi grazie a Proclo che in poche righe ci informa che Nicomede scoprì le curve concoidi, insieme alle loro proprietà e caratteristiche, e grazie a queste risolse il problema della trisezione dell´angolo. Il nome concoide deriva dal greco e significa simile ad una conchiglia, proprio perché la forma della curva ricorda quella di una conchiglia. La concoide di Nicomede godette di un notevole successo fra i matematici del XVII° sec. In un carteggio Fermat e Roberval completarono la ricerca sulle tangenti alla curva. Huygens giunse alla costruzione dei flessi applicando il metodo di Cartesio e lo stesso trovò che l´area tra i rami della curva è infinita. Addirittura Newton propose di includerla, insieme alla retta e alla circonferenza, tra le curve di cui un geometra dovrebbe sempre potersi servire.

 

 

Costruzione

 

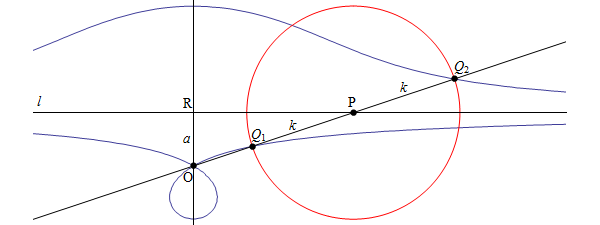
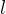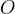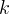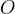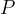Vediamo la costruzione della concoide. Sia data una retta , un punto non sulla retta ed una distanza . Tracciamo una retta passante per il punto e un qualsiasi punto sulla retta 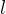. Chiameremo concoide di Nicomede il luogo dei punti 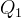e 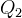sulla retta 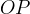, tali che i segmenti 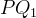e 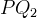siano uguali a 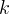, cioè 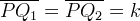al variare del punto 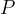sulla retta .

 

 

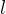Equazioni

Preso per polo di un sistema di coordinate polari il punto 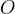, come asse polare la perpendicolare ad 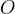su 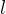e detto 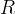il punto d´intersezione fra queste due rette chiameremo 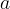la distanza 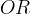. Possiamo rappresentare la curva in coordinate polari 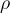e 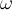con la seguente equazione:

 

 

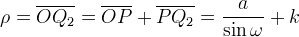
Passando a coordinate cartesiane con i ben noti cambiamenti di variabili 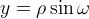e 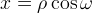si ottiene:

 

 

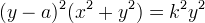
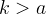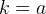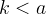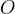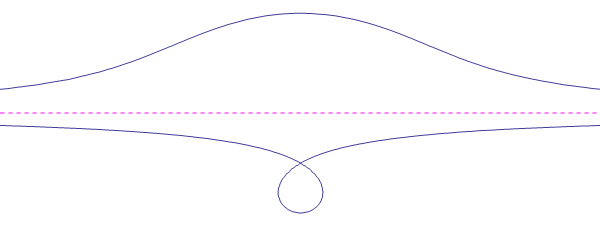
da cui si evince che la concoide di Nicomede è una curva del quart´ordine. Bisogna notare che a seconda che si scelga , , , la curva ha in un punto doppio e precisamente un nodo, una cuspide, un punto isolato. Nelle figure seguenti sono rappresentati i tre casi:

 

 

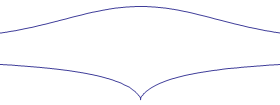
Dall´ultimo di questi tre casi si capisce pił facilmente come mai alla curva sia stato attribuito il nome concoide, cioè a forma di conchiglia, come si può vedere chiaramente dalla figura qui sotto:

 

 

 

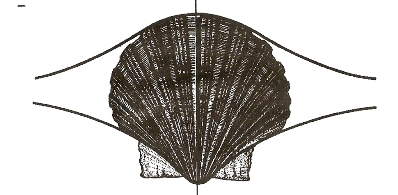
Proprietà

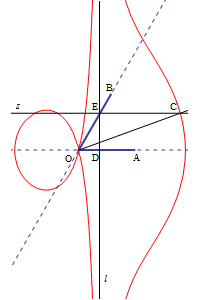
La curva, come detto, può essere usata per risolvere il problema della trisezione dell´angolo. Vediamo come: dato un angolo acuto , vogliamo costruire un angolo che sia 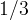dello stesso. Per prima cosa tracciamo una retta 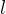che attraversa il segmento 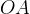e sia perpendicolare ad esso. Sia 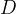l´intersezione tra la retta ed il segmento 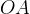, 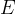l´intersezione tra la retta ed il segmento 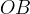. Tracciamo una concoide di Nicomede con retta 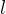punto non sulla retta 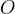e distanza 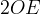. Tracciamo ancora una linea passante per 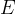e perpendicolare ad 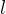. 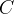Sia l´intersezione della retta con il ramo della concoide di Nicomede in cui non si trova il polo 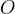. L´angolo è tre volte l´angolo . Ovviamente la costruzione del punto 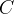non può essere fatta con il solo ausilio di riga e compasso, poichè la stessa concoide non può essere costruita solo con riga e compasso. Da notare che, contrariamente a quanto accade con altre curve trisettrici, per la trisezione di un angolo c´è bisogno di una nuova concoide ogni volta.

La stessa curva può essere usata per risolvere il problema della duplicazione del cubo.

Alcune proprietà matematiche sono che la curva ammette asintoto di equazione 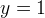e che l´area compresa fra i due rami della curva è infinita.

La concoide di Nicomede è la cissoide di una circonferenza con polo nel centro della circonferenza.

Inoltre la concoide di Nicomede trovò applicazione in architettura nella delineazione dei fusti delle colonne: la sezione verticale di queste aveva la forma dell´anello della concoide.

Come per la cissoide nel tempo il nome concoide ha assunto il significato di un metodo per la costruzione di curve: ad esempio se al posto della retta si considera una circonferenza e per polo si prende un punto qualsiasi sulla circonferenza si ottiene la lumaca di Pascal.