LA LUMACA DI PASCAL
Storia
La lumaca, o chiocciola, di Pascal prendo appunto il nome dal matematico francese Etienne Pascal, padre del più famoso Blaise Pascal, che per primo ne definì proprietà e caratteristiche. Tuttavia sembra che la curva fosse già nota nel 1200 a Giordano di Nemore, e forse anche agli antichi greci. Anche il pittore, scultore (e matematico) tedesco Albrecht Dürer, nel 1525, pubblicò un libro in cui era presente, insieme a numerose altre curve, la lumaca. Il nome fu coniato per la curva dal matematico francese Roberval, nel 1650, per la sua forma simile ad un guscio di lumaca.
Costruzione
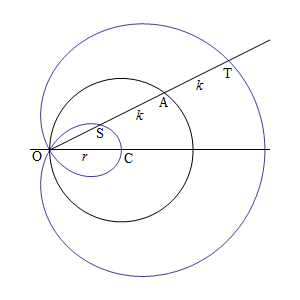
La lumaca di Pascal viene solitamente descritta come la concoide di un cerchio rispetto ad un
punto sulla sua circonferenza. Vediamo come: prendiamo un punto fisso 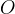 sulla circonferenza
e sia
sulla circonferenza
e sia 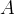 un punto qualsiasi sulla circonferenza. La lumaca di Pascal è il luogo dei
punti
un punto qualsiasi sulla circonferenza. La lumaca di Pascal è il luogo dei
punti 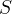 e
e 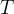 tali che le distanze
tali che le distanze
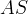 e
e 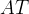 siano uguali a una costante
siano uguali a una costante
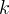 , ovvero
, ovvero 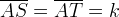 , al variare del punto
, al variare del punto
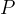 sulla circonferenza.
sulla circonferenza.
Equazioni
Se prendiamo le coordinate polari 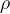 e
e
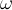 , rispettivamente corrispondenti nella figura, ad
, rispettivamente corrispondenti nella figura, ad 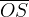 e
e 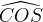 , dove
, dove 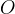 è il polo e
è il polo e
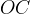 l´asse polare, si ha:
l´asse polare, si ha:
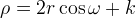
dove  è il raggio fissato della circonferenza interna usato per descrivere la
lumaca, mentre
è il raggio fissato della circonferenza interna usato per descrivere la
lumaca, mentre 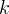 è la costante considerata. Da questa si
ottiene, con i tipici cambiamenti di coordinate, la seguente equazione cartesiana:
è la costante considerata. Da questa si
ottiene, con i tipici cambiamenti di coordinate, la seguente equazione cartesiana:
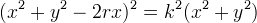
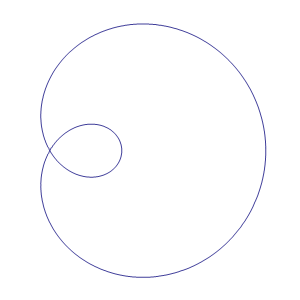
da cui si evince che la lumaca è una quartica. Bisogna distinguere tre casi: se
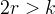 , la curva si presenta, nella forma usuale, con un anello interno e ha quindi un punto
doppio nel punto
, la curva si presenta, nella forma usuale, con un anello interno e ha quindi un punto
doppio nel punto 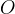 ; se
; se 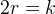 la
lumaca ha un cuspide nel punto
la
lumaca ha un cuspide nel punto 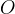 ; infine se
; infine se
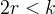 la lumaca un punto isolato in
la lumaca un punto isolato in
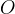 (sotto si possono vedere i tre casi). In particolare se
(sotto si possono vedere i tre casi). In particolare se
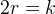 la curva ha assunto nel tempo il nome di
"cardioide": la curva fu studiata da Romer (1674), poi dal
matematico de La Hire, allievo di Desargues, che nel 1708 nè
trovò la lunghezza, mentre nel 1741 fu de Castillon ad attriburle questo nome per la sua forma
simile a quella di un cuore.
la curva ha assunto nel tempo il nome di
"cardioide": la curva fu studiata da Romer (1674), poi dal
matematico de La Hire, allievo di Desargues, che nel 1708 nè
trovò la lunghezza, mentre nel 1741 fu de Castillon ad attriburle questo nome per la sua forma
simile a quella di un cuore.

|

|

|
Proprietà
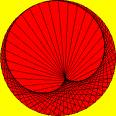
Vediamo alcune proprietà della curva. Innanzi tutto la curva può essere ottenuta in molti modi: come inviluppo di
circonferenze (ovvero è tangente ad una famiglia di circonferenze); si può anche ottenere facendo ruotare una
circonferenza su un´altra circonferenza e considerando la curva data da un punto sulla circonferenza ruotante (nel caso
della cardioide). Una proprietà molto importante è che la
lumaca di Pascal risolve il problema del ponte levatoio, problema meccanico, risolto per primo dal
marchese de l´Hopital, poi anche da altri. Nel caso della
cardioide la curva fu presa in considerazione da Romer per essere
utilizzata per i denti degli ingranaggi meccanici. Altra proprietà della lumaca, di cui sembra
si sia accorto per primo proprio Blaise Pascal, è che essa risolve il problema della trisezione
dell´angolo nel caso 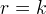 . Infine, come possiamo vedere sotto la
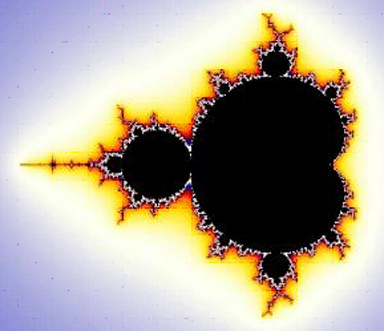
cardioide compare come figura centrale nel famoso frattale di Mandelbrot, e in generale ogni
"mini-insieme" del frattale contiene una cardiode.
. Infine, come possiamo vedere sotto la
cardioide compare come figura centrale nel famoso frattale di Mandelbrot, e in generale ogni
"mini-insieme" del frattale contiene una cardiode.