LA SPIRALE DI ARCHIMEDE

Storia
La spirale di Archimede fu scoperta dal grandissimo matematico (e non solo) siracusano ed esposta per la prima volta nel suo trattato "Sulle spirali" indirizzato a Dositeo, matematico di Alessandria; tuttavia tracce della spirale si trovano già in alcuni dipinti minoici risalenti al 1650 a.C. Nonostante probabilmente i minoici non fossero a conoscenza delle proprietà della curva, tuttavia la loro rappresentazione è sorprendente poichè la spirale di Archimede non si trova in natura a differenze di altri tipi di spirali che si incontrano per esempio in alcune conchiglie.
Successivamente Pappo fu indotto erroneamente ad attribuire a Conone di Samo, discepolo di Archimede, la scoperta della spirale, poichè il maestro siracusano inviò a Conone, prima della stesura definitiva del trattato, alcuni teroemi intorno alla spirale. Grandi studiosi del calibro di François Viète e Galileo furono attratti dal fascino della spirale. Successivamente Pascal riuscì a risolvere l´arduo compito della rettificazione della spirale, sostanzialmente riconducendendo il problema all´analogo di quello sulla parabola.

Costruzione
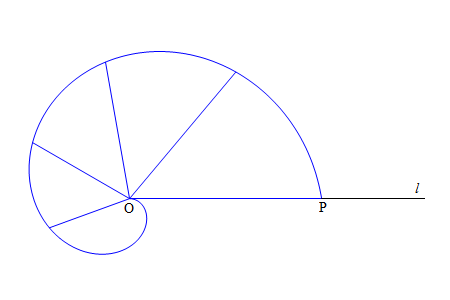
Nel suo libro "Sulle spirali" Archimede dà una descrizione cinematica della
curva: una retta 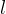 che ha un estremità fissata in
che ha un estremità fissata in
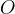 ruota uniformemente; su di essa si muove di moto uniforme un punto
ruota uniformemente; su di essa si muove di moto uniforme un punto
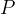 . La curva descritta dal punto
. La curva descritta dal punto 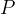 è la spirale di Archimede.
è la spirale di Archimede.
Equazioni
Dalla descrizione si capisce che in ogni punto il raggio è direttamente proporzionale all´angolo, quindi si ottiene la seguente equazione:
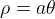
dove 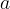 è una costante che possiamo assumere positiva. La
spirale di Archimede è una curva trascendentale. Come nella figura iniziale, la curva viene
rappresentata usualmente con i valori di
è una costante che possiamo assumere positiva. La
spirale di Archimede è una curva trascendentale. Come nella figura iniziale, la curva viene
rappresentata usualmente con i valori di 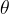 compresi nell´intervallo
compresi nell´intervallo
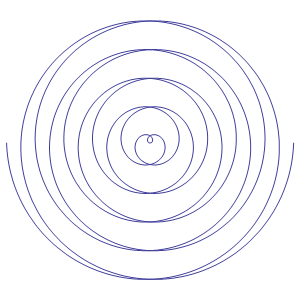
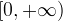 , mentre nella prima curva sotto a sinistra si può
vedere la rappresentazione irriconoscibile della spirale di Archimede nell´intervallo
, mentre nella prima curva sotto a sinistra si può
vedere la rappresentazione irriconoscibile della spirale di Archimede nell´intervallo
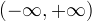 , in cui la curva assume infiniti punti doppi
sull´asse
, in cui la curva assume infiniti punti doppi
sull´asse 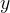 . Nella seconda figura a destra possiamo vedere,
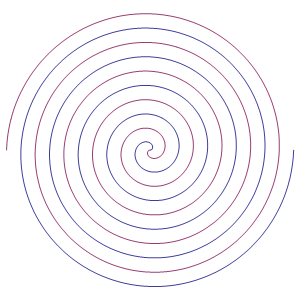
invece, un´altra classica rappresentazione, ovvero quella in cui vengono affiancate la curva
. Nella seconda figura a destra possiamo vedere,
invece, un´altra classica rappresentazione, ovvero quella in cui vengono affiancate la curva
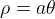 (in blu) e
(in blu) e
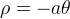 (in viola) entrambe nell´intervallo
(in viola) entrambe nell´intervallo
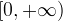
|
|
Proprietà
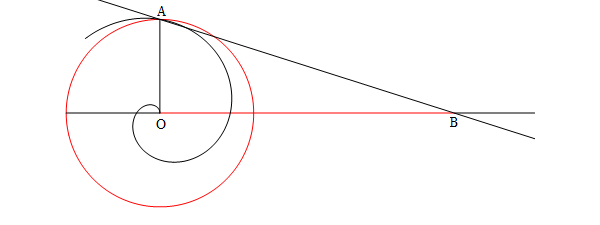
Grazie alla spirale, Archimede riuscì a quadrare la
circonferenza. Nell´opera "Sulle spirali", nella proposizione 18, egli (in termini moderni) scrive: supponiamo la
retta ruotante 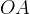 abbia compiuto un giro completo e si prenda la tangente alla
spirale in questo punto; dal centro di rotazione si tracci la perpendicolare alla retta
abbia compiuto un giro completo e si prenda la tangente alla
spirale in questo punto; dal centro di rotazione si tracci la perpendicolare alla retta
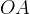 : il segmento di perpendicolare
: il segmento di perpendicolare 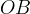 compreso fra il centro di rotazione e il punto di intersezione fra la perpendicolare e la tangente è uguale alla
circonferenza del "primo cerchio", ovvero il cerchio che ha come raggio il segmento compreso fra il centro di rotazione
e il punto di tangenza. Archimede dunque riduce il problema a quello di traciare la tangente alla
spirale. Grazie alla spirale è inoltre possibile trisecare un
qualsiasi angolo. La concoide di una spirale di Archimede è ancora una
spirale di Archimede.
compreso fra il centro di rotazione e il punto di intersezione fra la perpendicolare e la tangente è uguale alla
circonferenza del "primo cerchio", ovvero il cerchio che ha come raggio il segmento compreso fra il centro di rotazione
e il punto di tangenza. Archimede dunque riduce il problema a quello di traciare la tangente alla
spirale. Grazie alla spirale è inoltre possibile trisecare un
qualsiasi angolo. La concoide di una spirale di Archimede è ancora una
spirale di Archimede.
La spirale ha moltissime applicazioni nella vita reale, vediamone alcune: la forma di alcune galassie è proprio quella di una spirale di Archimede; la traccia dei dischi in vinile è una spirale di Archimede; in idraulica le pompe di scorrimento per liquidi e gas sono formate da due spirali di Archimede della stessa grandezza; in ambito militare, muoversi in un percorso a forma di spirale di Archimede è una tecnica di ricerca per coprire tutta l´ area; infine in neurologia, chiedere a qualcuno di disegnare una spirale di Archimede è uno dei metodi per misurare una disfunzione motoria nella malattia di Parkinson.