LA QUADRATRICE DI IPPIA

 

 

Storia

La prima curva documentata nella storia della matematica (oltre il cerchio e la retta) è la quadratrice di Ippia. Ippia di Elide fu astronomo, matematico e sofista vissuto ad Atene nella seconda metà del V° secolo a.C. Egli si servì della quadratrice per risolvere il problema della trisezione dell´angolo e per questo la curva è anche nota come trisettrice. Successivamente, intorno alla metà del IV° secolo a.C., Dinostrato, geometra fratello di Menecmo, si servì della curva per risolvere il problema della quadratura del cerchio, da cui il nome di quadratrice. Tuttavia entrambi pensavano erroneamente che la curva si limitasse alla porzione compresa (nel moderno grafico in un piano cartesiano) nel primo quadrante in cui la 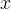varia tra 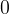e 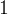. Questa convinzione rimase almeno fino a Viète, ovvero fino alla fine del XVI° secolo. Agli inizi del XVII° secolo sembra sia stato Roberval il primo ad accorgersi che la curva si poteva estendere come la conosciamo oggi.

 

 

Costruzione

 

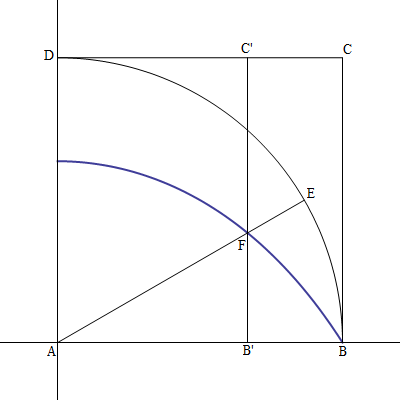
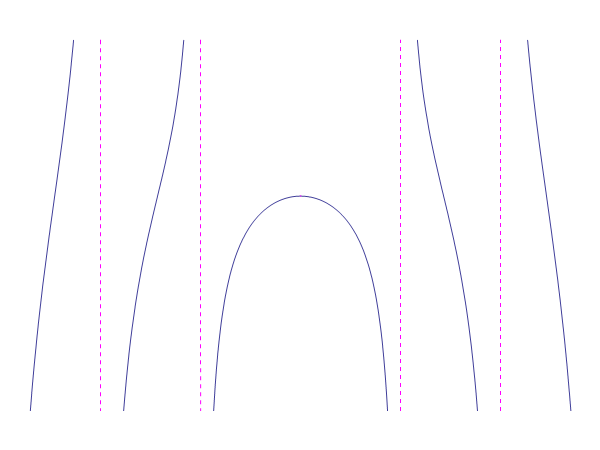
Vediamo come Pappo descrisse la curva, che Ippia e Dinostrato costruirono in modo meccanico: dato un quadrato 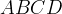si tracci con centro in 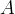il quarto di circonferenz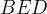a . Sia 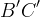un segmento parallelo all´asse 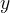che partendo dal segmento 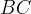si muova a velocità costante verso il segmento 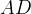. Sia ora 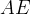il raggio della circonferenza che descriva uniformemente l´angolo 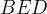da 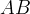fino ad 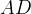. Entrambi i movimenti del segmento e del raggio iniziano e finiscono simultaneamente. Il luogo dei punti 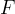intersezione del raggio 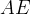e del segmento 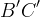è la quadratrice di Ippia.

 

 

Equazioni

Dalla costruzione precedente, dett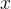e e 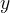le coordinate del punto 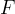, 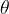l´angolo 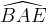, un parametro che varia nell´intervallo 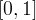e la lunghezza del lato del quadrato, si ottengono le seguenti equzioni parametriche:

 

 

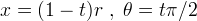
da cui eliminando il parametro si ottiene:

 

 

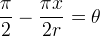
Ora usando la ben nota relazione 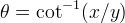si ottiene l´equazione cartesiana della quadratrice:

 

 

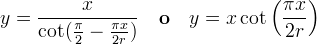
Le ultime due equazioni sono uguali grazie alla relazione .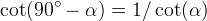

 

 

Proprietà

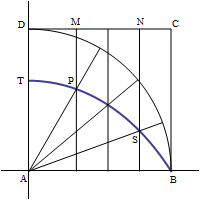
Abbiamo detto che Ippia utilizzò la curva per risolvere il problema della trisezione dell´angolo; vediamo come: supponiamo di voler trisecare, ad esempio, l´angolo 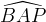(figura a destra). Per primo procediamo tracciando da 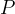la parallela a 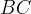che incontra il lato 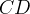nel punto 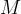. Successivamente divideremo il segmento 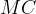in tre parti uguali 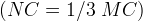e tracceremo la parallela a 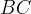partente dal punto fino all´intersezione con la curva nel punto . L´angolo 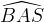è esattamente la terza parte dell´angolo .

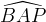Come detto della curva si servì anche Dinostrato per ottenere la quadratura del cerchio. Egli, infatti, dimostrò che il segmento 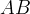è medio proporzionale tra l´arco 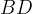e il segmento 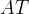: è così possibile ottenere un segmento rettilineo, della lunghezza dell´arco 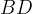, pari ad un quarto di circonferenza. Di qui è facile, con semplici costruzioni geometriche, arrivare ad un quadrato della stessa area di un cerchio di raggio .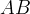

In entrambi i casi comunque restava il fatto che la quadratrice (o trisettrice) non era costruibile con il solo utilizzo di riga e compasso.