CURVE CELEBRI |
 |
 |
 |
 |
 |
|
|
|
|||||
LE CONICHE
Storia
Il più antico autore di cui abbiamo traccia, che abbia trattato delle coniche è Menecmo, matematico greco del IV° secolo a.C., maestro del grande condottiero Alessandro Magno. Esse furono utilizzate nel tentativo di risolvere uno dei tre famosi problemi dell´antichità: la duplicazione del cubo, detto anche "il problema di Delo".
Menecmo descrisse le coniche come intersezione di un cono circolare
retto, con angolo al vertice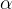 
variabile ed un piano fisso
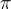perpendicolare alla direttrice 
del cono; a
seconda che sia abbia:
, 
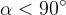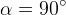oppure
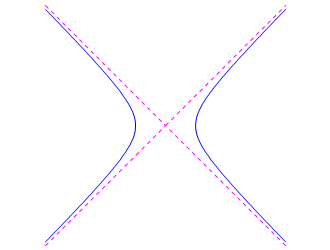
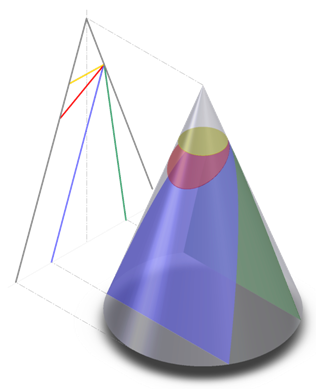
si otterrà rispettivamente un´ellisse, una parabola o un´iperbole.
Successivamente Apollonio, il Grande Geometra, vissuto a cavallo tra il III° e il II° secolo a.C., scrisse un trattato dal titolo proprio "Le Coniche". Apollonio ottiene le curve come intersezione di un cono fisso e un piano secante ad inclinazione diverse. Fu Apollonio ad attribuire alle curve il loro nome i quali derivano dal confronto fra due proprietà caratteristiche di ciascuna curva:
Apollonio, inoltre, sostituì il cono ad una falda con quello a due falde trovando il secondo ramo dell´iperbole. Come tutta la matematica, dopo una lunga pausa buia (inframezzata solo dall´intersse di Pappo), le coniche vedono una rinascita nel Seicento grazie a scenziati del calibro di Pascal, Cartesio, Wallis, ma soprattutto Galileo, Keplero, Newton, i quali scoprirono importantissime proprietà e applicazioni delle coniche a moltissimi campi della scienza.
Costruzione
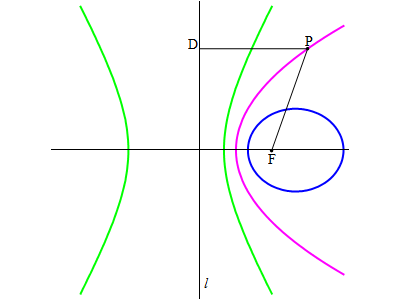
Oltre che come intersezione di un cono a due falde con un piano, le coniche possono essere
costruite nel modo seguente: sia data una retta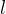 
ed un punto
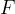non appartente alla retta 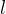. Ciascuna conica
può essere descritta come il luogo dei punti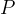 
tali che il rapporto tra la distanza
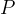di da 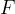con la distanza di
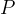da 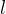sia costante. Ovvero detto
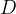il punto di intersezione tra la retta 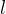e la
perpendicolare ad 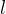passante per il punto 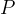si
ha:
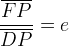
dove la costante 
viene detta eccentricità,
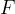fuoco e 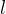direttrice della conica.
Se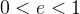 
la conica risultante è un´ellisse, se
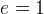una parabola, se 
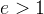un´iperbole.
Equazioni
Facendo riferimento alla costruzione precedente consideriamo le coordinate polari
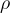e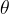 
, dove
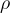è il segmento 
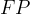e
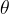è l´angolo compreso tra l´ass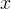e
e 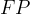. Ora prendendo per direttrice l´asse
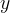e per fuoco il punto
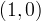si ha la seguente equazione polare per una
conica:
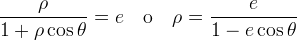
Se si vogliono ottenere equazioni cartesiane, dette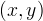 
le coordinate
del punto 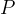, mantenedo la stessa direttrice e fuoco, e sfruttando la stessa relazione
usata per la costruzione, si ha:
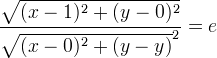
che diventa l´equazione cartesiana generale di una conica:
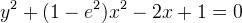
Proprietà
Come abbiamo detto le coniche furono utili a Menecmo per risolvere il
problema della duplicazione del cubo; vediamo come ci riuscì (in termini moderni). Partendo dal metodo di
Ippocrate della proporzione continua, considerando segmenti di lunghezza
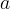e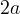 
:
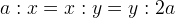
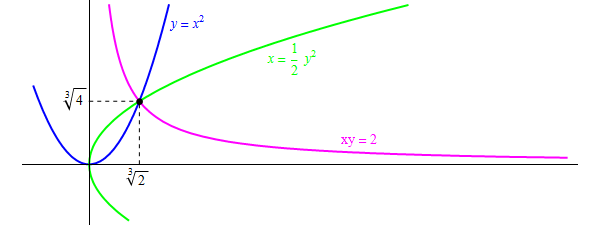
Menecmo otteneva, considerando le proporzioni a due a due, le equazioni:
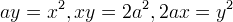
la prima e la terza, equazioni di una parabola, la seconda di una iperbole.
Mettendo queste a sistema a due a due, Menecmo otteneva la lunghezza del lato del cubo di volume
doppio, come si vede nella figura (dove abbiamo posto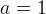 
).
Un´altra proprietà delle coniche, in geometria proiettiva, è che esse sono equivalenti, ovvero possono essere trasformate l´una nell´altra tramite una trasformazione proiettiva.
Le coniche trovano applicazione in ottica, sia in epoca ellenistica con la costruzione di specchi parabolici (specchi ustori, Faro di Alessandria), sia nel Seicento: Newton costruì un telescopio usando specchi parabolici e specchi ellittici (successivamente lo specchio ellittico venne sostituito con uno iperbolico).
L´utilizzo più rivoluzionario delle coniche fu in astronomia da parte del tedesco Keplero. Egli scoprì che i corpi celesti percorrono orbite date da sezioni coniche, e non come prima si pensava semplici circonferenze. Solo Newton successivamente riuscì a dimostrare la cosa come conseguenza delle leggi gravitazionali da lui scoperte (il problema è noto come "problema dei due corpi").