|
|
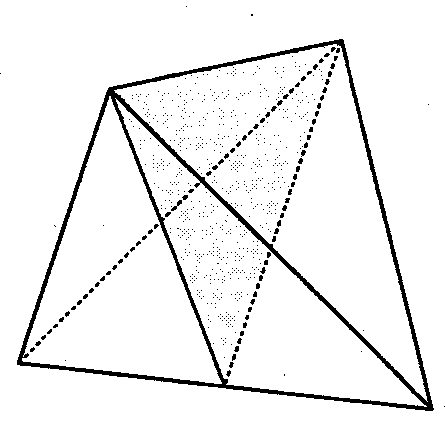 |
Piano di simmetria della riflessione individuato da uno spigolo e dal punto medio dello spigolo opposto
Ci sono 6 piani di quest tipo
|
|
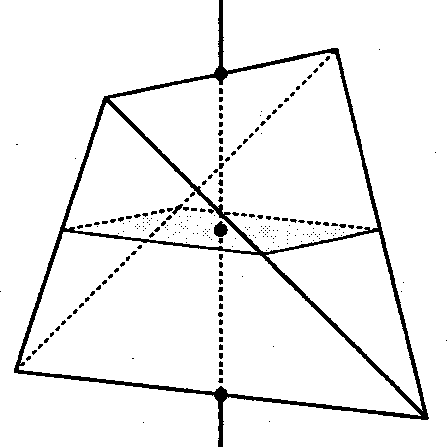 |
Asse di rotazione per i punti medi di due spigoli opposti
Piano di riflessione ortogonale a tale retta e passante per il centro del tetraedro
Gli assi per i punti medi di due spigoli opposti sono in tutto tre e le rotazioni possono essere di 90° o 270°
Abbiamo quindi in tutto 6 riflessioni rotatorie |
|
Il gruppo Γ(T) ha dunque 12 rotazioni, 6 riflessioni e 6 riflessioni rotatorie, cioè:
|
Osservazioni sulle rotazioni
Γ(C), Γ(I), Γ(T) contengono rispettivamente 24, 60, 12 rotazioni.
E' interessante osservare che il numero delle rotazioni non è casuale ma è esattamente il doppio del numero degli spigoli del poliedro che si prende in considerazione

|



