1. La prima osservazione da fare è che le radici quadrate complesse di i sono due. Una base di C come Q-spazio vettoriale è {1,i} dunque per scrivere u in forma normale bisogna determinare due numeri razionali a e b tali che u risulti uguale ad a+ib. Noto che la somma "+" definita sul gruppo abeliano del campo complesso è termine a termine e noto che, banalmente, la coppia (a₂,b₂) associata a -i è (0,-1), resta da trovare la coppia (a₁,b₁)∈Q² tale che ω=a₁+ib₁.

Le radici quadrate complesse di i=cos(π/2)+i·sen(π/2) sono due, e il loro modulo è dato dalla radice quadrata del modulo di i, cioè 1, mentre l'argomento è rispettivamente π/4 e 5π/4. Quindi: ω=√2/2+i√2/2 e l'altra radice è -√2/2-i√2/2. Dunque infine:

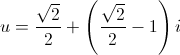
2. Si ha: u=ω-i  ⇒  (u+i)²=i  ⇒  u²+2iu-1=i  ⇒  (u²-1)²=[i(1-2u)]²=-(1-2u)²  ⇒  u⁴-2u²+1=-(1-4u+4u²)  ⇒  u⁴+2u²-4u+2=0

da cui il polinomio a coefficienti razionali, monico ed irriducibile (vedi sotto) che si annulla in u, dunque polinomio minimo di u su Q è:

Irriducibilità di p_u. Primo modo. Per il criterio di Eisenstein con p=2.

Secondo modo. Il polinomio è di quarto grado, non biquadratico, questo caso può sembrare più difficile degli esercizi 6, 7, 8 (e 12) ma si risolve in meno passaggi. Da (a): ω=√2/2+i√2/2 e: u=√2/2+i(√2/2 - 1) e ponendo:

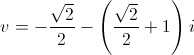
si ha che anche v verifica (v+i)²=i, quindi p_u(v)=0 ed, essendo u e v non reali, le quattro radici complesse del polinomio sono proprio u, v ed i loro complessi coniugati.

Ragionando come nell'esercizio 7 o 24 si trova che p_u è irriducibile in Q[x].

---

Torna agli esercizi.

Torna alla teoria.

Vai all'esercizio 10.