Soluzione
25.
Innanzitutto
si ha: u=cos(4π/3)+i·sen(4π/3)=-1/2-i·√3/2.
- Ogni numero complesso α
è algebrico
su R; se α
non appartiene ad R,
esso è radice di x²-2Re(αx)+∣α∣²∈R[x]. Il numero
complesso u è una radice cubica
complessa di 1.
- u=-1/2-i·√3/2
⇒ (u+½)2=-¾
⇒ u2+u+1=0
e:
pu(x)=x2+x+1
è monico, irriducibile (il discriminante: Δ=-3
non è un quadrato in R),
a coefficienti interi e dunque reali e si annulla in u,
cioè è il polinomio
minimo di u su R. Oppure: u,
essendo una radice terza di 1, verifica u3-1=0,
ed: u3-1=(u-1)(u2+u+1);
u ed ū sono le radici complesse e non reali di u2+u+1.
- Vediamo se questo campo è il campo
complesso. Sicuramente R(-1/2-i·√3/2)⊆R(i)
in quanto -1/2-i·√3/2∈R(i)=C.
Per
l'altra inclusione risulta allo stesso modo che C⊆R(-1/2-i·√3/2)
perchè i∈R(-1/2-i·√3/2),
infatti:
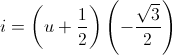
.
- Essendo u algebrico
su R,
è anche algebrico su una qualunque estensione
di R,
mentre non è detto che lo sia su un sottocampo,
per esempio Q.
In questo caso però il polinomio minimo pu(x)
di u su R
è a coefficienti interi, quindi razionali. Il fatto che
esso è monico e si annulla in u
è inalterato, ed essendo irriducibile su R lo è
anche su Q,
quindi pu è
anche il polinomio minimo di u sui razionali, e
u è algebrico su Q.
- Per quanto detto nel punto (d),
il polinomio minimo di u su Q è pu.
Il grado di Q(u)/Q è, come
quello di R(u)/R, deg(pu(x))=2.
- Si ha che R(u)/Q(u)
è estensione
trascendente non essendo, per esempio, π algebrico su Q(u).
Infatti se lo fosse, ci sarebbe un polinomio diverso da 0 a coefficienti in Q(u)
nullo in π. Ma Q(u)={a+bu,
a,b∈Q},
quindi esisterebbero ai,
bi con i=0,...,n
tali che (a0+b0u)+(a1+b1u)π+...+(an+bnu)πn=0
cioè (a0+a1π+...+anπn)+u(b0+b1π+...+bnπn)=0
e questo accade in Q(u)
se e solo se a0+a1π+...+anπn=0
o b0+b1π+...+bnπn=0
con qualche ai o bi
diverso da 0 cioè π sarebbe algebrico su Q, il che
è falso.
Torna
agli esercizi.
Torna
alla teoria.
Vai
all'esercizio 26.

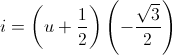 .
.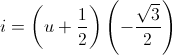 .
.