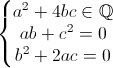
Mostrare: q∈Q, √q∈Q(∛2) ⇒ √q∈Q. Vediamo due possibili soluzioni, soluzione A e soluzione B.
A. Innanzitutto (vedi soluzione 20a) Q(∛2) è estensione finita del campo dei razionali di grado 3, con base: {1, ∛2, ∛4}.
Per la seconda ipotesi si ha: √q∈Q(∛2) ⇒ √q=a+b∛2+c∛4 da cui, elevando e raccogliendo: q=(a2+4bc)+2(ab+c2)∛2+(b2+2ac)∛4. Quindi per la prima ipotesi: (a2+4bc)+2(ab+c2)∛2+(b2+2ac)∛4∈Q. Quest'ultima condizione si può esprimere con il sistema:
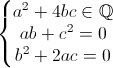
Per la seconda equazione si hanno ora due casi:
a=0,
c=0 ⇒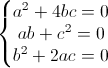 
⇒ √q=0=q
mentre se:
b=0,
c=0 ⇒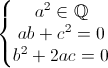 
dunque:
q=a2∈Q ⇒ √q=a∈Q
B. Se q∈Q e √q∉Q, allora Q(√q) grado 2 su Q perchè il polinomio minimo di √q su Q è x2-q. Quindi, se √q∈Q(∛2), si ha: Q(√q)⊆Q(∛2) da cui:
[Q(∛2):Q(√q)]·[Q(√q):Q]=[Q(∛2):Q]
Il campo Q(∛2) ha grado 3 su Q, dato che il polinomio minimo di √q su Q è x3-2. Infatti su C:
x3-2=(x-∛2)(x-∛2e2πi/3)(x-∛2e4πi/3)
dove ∛2·e2πi/3 e ∛2·e4πi/3 sono le due radici cubiche complesse primitive di 1. Dunque il polinomio x3-2 non ha radici in Q ed essendo di terzo grado questo ci dice che è irriducibile su Q, inoltre è monico e si annulla in ∛2. Allora se valesse l'equazione data dal tower lemma si avrebbe che 2 divide 3 il che, in Z, non è possibile.
Torna agli esercizi.
Torna alla teoria.
Vai all'esercizio 23.
