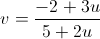Soluzione 18.


  1. Si ha: u=∛4  ⇒  u3=4  ⇒  u3-4=0

Il polinomio x3-4 è a coefficienti razionali (interi) ed è monico, irriducibile, avendo due radici complesse ed una reale di cui nessuna razionale, non ha un fattore lineare in Q[x] e si annulla in u, dunque esso è il polinomio minimo di u su Q.



  1. Il grado del polinomio minimo di u su Q è 3, quindi una base è: {u0, u, u2}={1, ∛4, ∛16}={1, ∛4, 2∛2} oppure anche: {1, ∛2, ∛4} (da cui si ha anche l'ulteriore risultato: Q(∛4)=Q(∛2)).


  1. Basta provare che u∈Q(v) e che v∈Q(u), perchè allora Q(u)⊆Q(v) e Q(u)⊆Q(v) cioè vale l'uguaglianza. Ma v∈Q(u) perchè Q(u) è un campo contenente Q e:

.

mentre u∈Q(v) perchè:



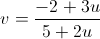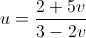
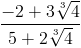  1. Scriviamo: v= in forma normale in Q(u) quindi rispetto alla base (1, u, u2). In un'estensione di campi di grado 3 questo comporta una difficoltà in più rispetto agli esercizi 14 e 15 ma, noto che: a3+b3=(a+b)(a2+b2-ab) per ogni a e b reali, si ha: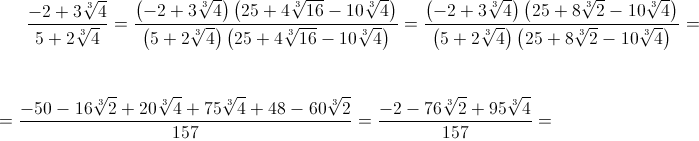







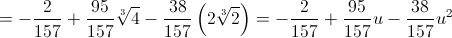
Torna agli esercizi.

Torna alla teoria.

Vai all'esercizio 19.