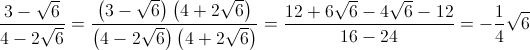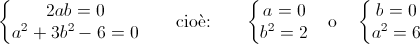Soluzione
14.
- Si ha:
ovvero:
a+b√6 con a=0
e b=-1/4, entrambi razionali.
- Si cercano
coppie (a,b) e (c,d) di
razionali che verifichino la: a+b√3=c+d√6.
Essendo
Q contenuto
sia in Q(√3)
che in Q(√6),
si ha: Q⊆(Q(√3)∩Q(√6)).
Scrivendo poi la: a+b√3=c+d√6
come: (a-c)+(b-d√2)√3=0 si
osserva che non esistono altre coppie di razionali che verificano,
quindi Q
è non solo contenuto ma coincide con l'intersezione delle sue due
estensioni.
- Ricordiamo che Q(√3,√6)=Q(√3)(√6).
Si ha: [Q(√3):Q]=2
perchè il polinomio
minimo di √3 su Q è x2-3
(monico, razionale, irriducibile perchè
senza radici
in Q). [Q(√3)(√6):Q(√3)]=2
perchè il polinomio minimo di √6
su Q(√3)
è x2-6
(monico, a coefficienti in Q(√3),
irriducibile su Q(√3)).
Basta provare che le sue radici non stanno in Q(√3)={a+b√3,
a,b∈Q}.
Cerchiamo gli a,b∈Q tali che (a+b√3)²=6
cioè: (a2+3b2-6)+2ab√3=0
che in Q(√3)
è equivalente a:
senza
soluzioni in Q.
Quindi
per il teorema della torre
si ha: [Q(√3,√6):Q]=[Q(√3)(√6):Q]=[Q(√3)(√6):Q(√3)]·[Q(√3):Q]=2·2=4.
Torna
agli esercizi.
Torna
alla teoria.
Vai
all'esercizio 15.