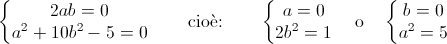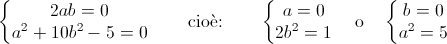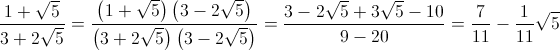Soluzione 15.

1. I campi Q(√5) e Q(√10) sono isomorfi come gruppi abeliani additivi. Se esistesse una φ isomorfismo di anelli si avrebbe: φ(1)=1 e dunque Q verrebbe mandato da φ identicamente in sè stesso, per definizione di morfismo, cioè: φ(a)=a per ogni a∈Q. Si ha: Q(√10)={a+b√10, a,b∈Q}. Se φ(√5)=a+b√10 allora 5=φ(5)=(φ(√5))²=a²+10b²+2ab√10 che in Q(√10) è equivalente a:

2. In modo perfettamente analogo alla soluzione dell'esercizio 14:

Torna agli esercizi.

Torna alla teoria.

Vai all'esercizio 16.