Determinare per quali valori del parametro reale
le seguenti serie sono convergenti
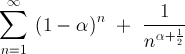
Possiamo riscrivere la serie di partenza come:
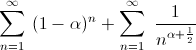
Per i risultati visti nella sezione "Teoria" sappiamo che se queste due serie sono convergenti allora anche la serie somma lo è.
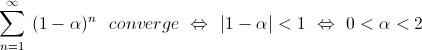
in quanto è la serie geometrica
di ragione (1-).
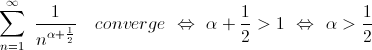
in quanto è la serie armonica generalizzata
di esponente ( + 1/2).
In definitiva per appartenente
all'intervallo ]0,5;2[ la serie data è convergente.
Si noti che se è positivo
ma più piccolo di 1/2 la serie data è a termini positivi
e non può convergere in quanto prevale il secondo addendo ovvero la parte armonica della serie.