Per partizione di un intervallo [a,b] intendiamo una sequenza finita 
; ciascun elemento [xi, xi + 1] è detto un sottointervallo che compone questa partizione. La lunghezza del più lungo di questi sottointervalli è detta ampiezza della partizione.
Una partizione segnata è una partizione alla quale associamo una certa sequenza di punti t0, ... , tn-1 appartenenti ciascuno al proprio corrispondente sottointervallo.
Definiamo inoltre, poiché ci sarà utile in seguito, il concetto di raffinamento: una partizione si dice più fine (o raffinamento) di un'altra se essa ne contiene tutti i punti. Nel caso di partizioni segnate, la sequenza di punti associata alla partizione più fine deve inoltre contenere tutti i punti della sequenza associata alla partizione meno fine. È banale osservare che un raffinamento di una partizione ha un'ampiezza minore o uguale all'originale.
Somma di Riemann
Supponiamo di avere una funzione reale f definita sull'intervallo [a,b], e stabiliamo una partizione segnata di tale intervallo. Si definisce allora somma di Riemann la quantità:
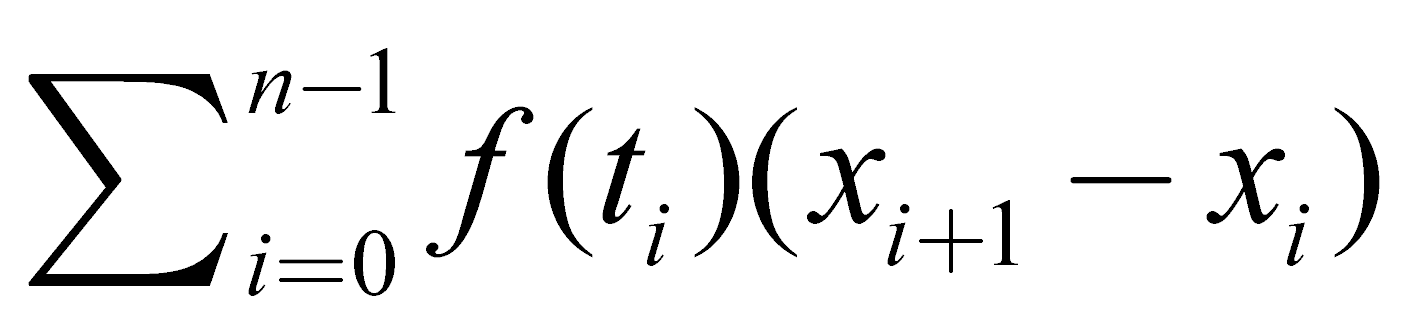
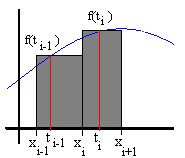
Tale somma è caratterizzata da come i punti tn sono stati scelti:
- se ti = xi essa si dice somma sinistra di Riemann
- se ti = xi+1 essa si dice somma destra di Riemann
- se ti = (xi+1+xi)/2 essa si dice somma media di Riemann
La media delle somme sinistra e destra è talvolta detta somma trapezoidale; è più accurata di entrambe, ma non ne faremo uso in queste pagine.
Si definiscono inoltre come somma superiore (o inferiore) di Darboux le espressioni che si ottengono sostituendo a f(ti) rispettivamente l'estremo superiore o l'estremo inferiore di f(ti) in ciascun intervallo. Vedremo come queste somme si riveleranno importanti ai fini dell'integrazione.