Sia f(x) una funzione definita sui reali, a valori reali e a supporto compatto (ossia che assume valori non nulli solo in un intervallo limitato [a, b]). Indichiamo inoltre con P una qualunque partizione segnata sull'intervallo [a,b] di cui sopra, di ampiezza δ.
Si può allora definire l'integrale di Riemann come il limite della somma di Riemann di f su P per δ che tende a zero, ossia: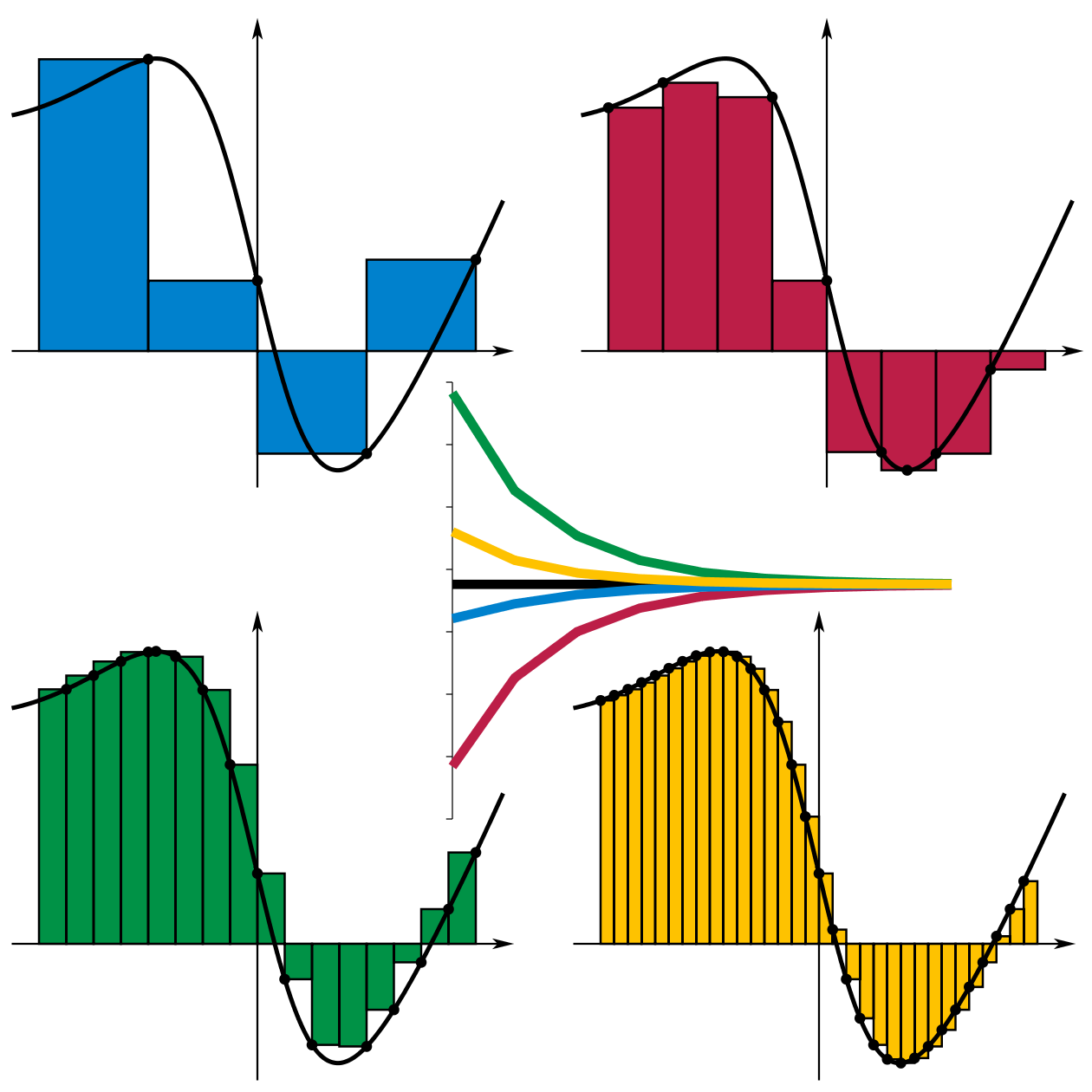
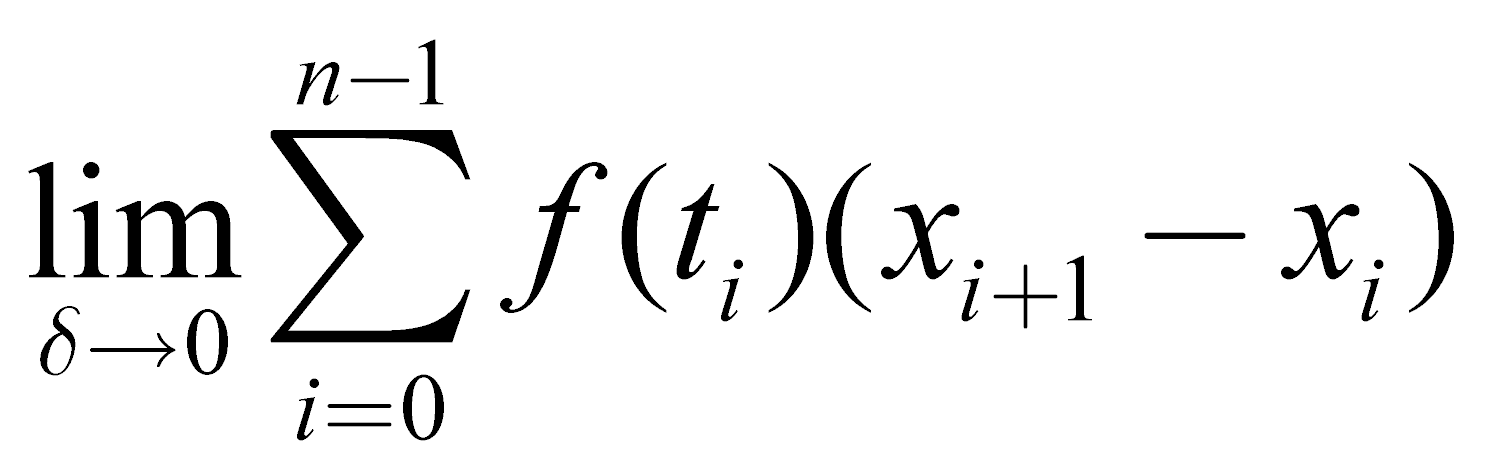
e la funzione f si dice Riemann integrabile se e solo se questo limite esiste, che si indica quindi con la notazione
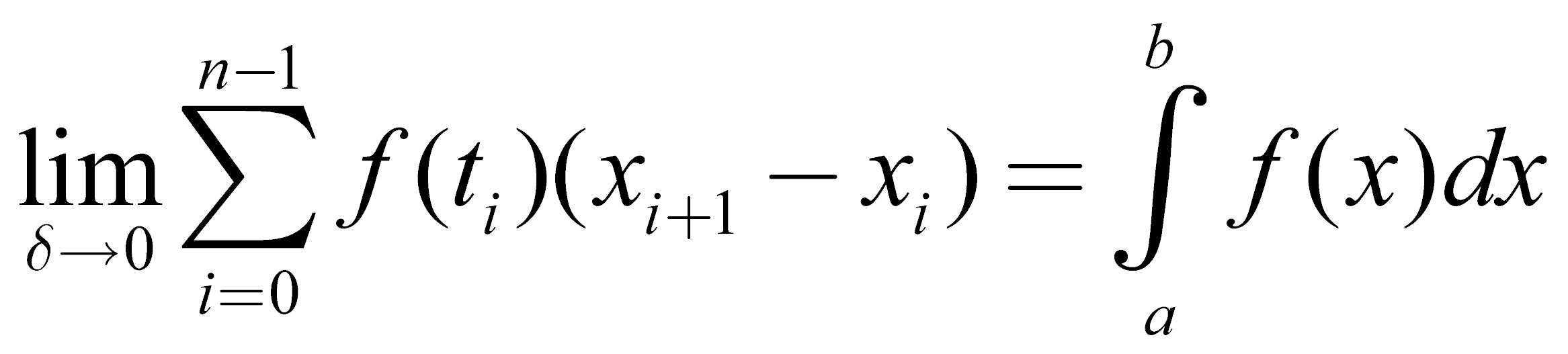
Tale definizione è la più corretta, tuttavia non è la più utile ai fini pratici, poiché il limite sull'ampiezza della partizione spesso non si presta a comode osservazioni. Fortunatamente essa è equivalente a quella dell'integrale di Darboux - che non a caso in moltissimi libri viene utilizzato al posto e col nome dell'integrale di Riemann.
Indichiamo con s(P) e S(P) rispettivamente le somme inferiori e superiori di Darboux di f su P. Consideriamo le possibili partizioni di [a, b] e indichiamo con L l'estremo superiore delle possibili somme inferiori e con U l'estremo inferiore delle somme superiori, ossia:
L = sup {s(P) : P è una partizione di [a, b]}, detto integrale inferiore di Darboux
U = inf {S(P) : P è una partizione di [a, b]}, detto integrale superiore di Darboux
Allora, se L = U, la funzione si dice Darboux integrabile e tale valore è il suo integrale di Darboux.
È facile verificare che le due definizioni sono equivalenti. Infatti, ricordando che tutte le somme di Riemann sono comprese tra le somme inferiore e superiore di Darboux:
- se l'integrale di Darboux esiste, devono esistere partizioni che producono somme inferiori e superiori di Darboux arbitrariamente vicine l'una all'altra, e quindi si possono ottenere su tali partizioni somme di Riemann convergenti.
- viceversa, osserviamo che è possibile scegliere e segnare una partizione in modo da ottenere una somma di Riemann arbitrariamente vicina ad una somma inferiore o superiore di Darboux sulla stessa partizione, e ciò continua a valere se operiamo una successione di raffinamenti su di essa. Se l'integrale di Riemann esiste, ogni tale successione converge all'azzerarsi dell'ampiezza, e con esse convergono anche gli integrali superiori ed inferiori di Darboux.