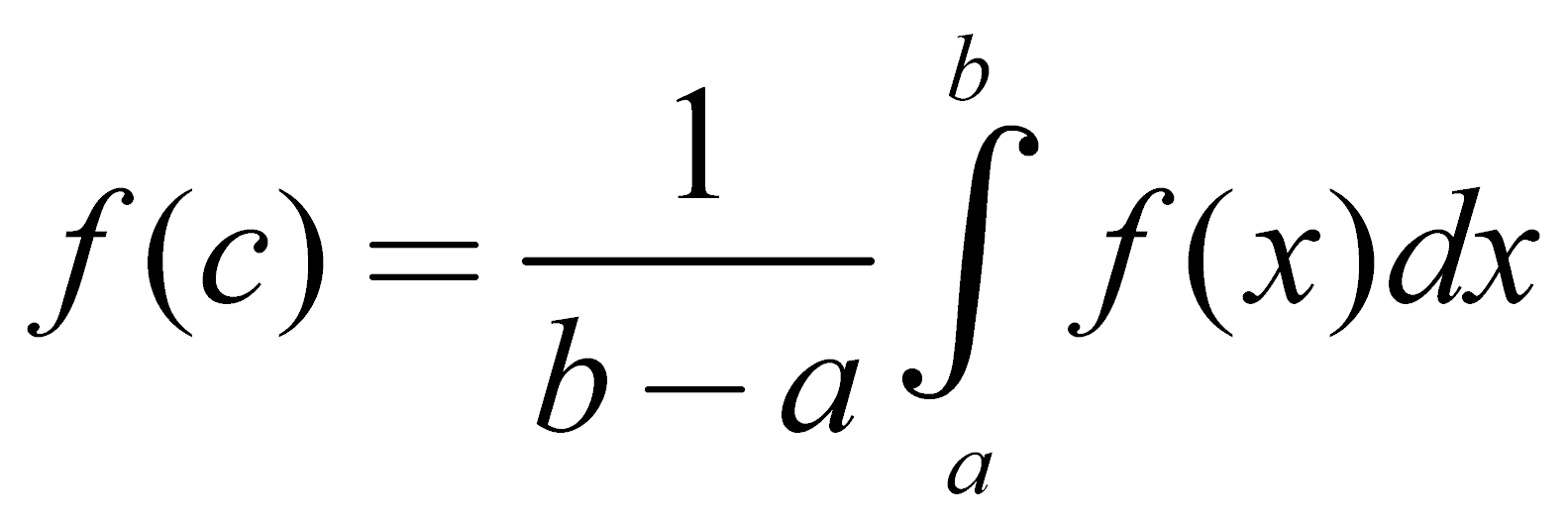Elenchiamo alcune proprietà e risultati basilari riguardanti l'integrale di Riemann:
- Criterio di integrabilità
- Una funzione reale è Riemann integrabile se e solo se è limitata e quasi ovunque continua.
- Linearità
- Se f e g sono Riemann integrabili, allora αf+βg, dove α e β sono costanti reali, è anch'essa Riemann integrabile e il suo integrale è la somma degli integrali di f e g.
- Rispetto della convergenza uniforme
- Se fn è una sequenza di funzioni Riemann integrabili che converge uniformemente ad una funzione f, allora f è Riemann integrabile e il suo integrale è il limite degli integrali delle funzioni fn.
- Isotonia
- Se f e g sono Riemann integrabili e f ≤ g, allora anche l'integrale di f è minore o uguale all'integrale di g.
- Valore assoluto
- Il modulo dell'integrale di una funzione f è minore o uguale all'integrale del modulo di f.
- Teorema della media
- Se una funzione reale f di dominio [a,b] è continua, allora esiste un punto c nel dominio tale che