Funzione di Dirichlet
Questa è senza dubbio la funzione più comune nello studio dell'integrale di Riemann - o meglio, dei suoi punti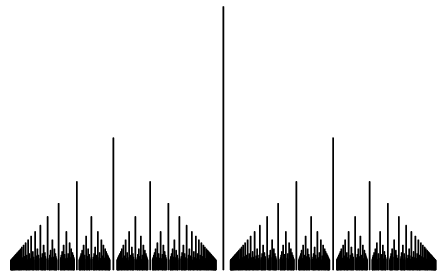 
deboli. Essa è definita avente valore zero in corrispondenza dei punti irrazionali compresi fra 0 e 1, e valore uno in corrispondenza di quelli razionali.
Il problema è palese se seguiamo la definizione di Darboux: essendo infatti sia i razionali che gli irrazionali sottoinsiemi densi del dominio [0,1], qualunque sottointervallo di qualunque partizione conterrà sia punti aventi valore zero che aventi valore uno; dunque le somme inferiore e superiore di Darboux continueranno a valere rispettivamente 0 e 1 a prescindere da quanto si raffini la partizione, e i rispettivi integrali non convergeranno mai.
Attenendosi alla definizione di Riemann l'osservazione è quasi altrettanto ovvia. Si costruiscono due successioni di partizioni segnate via via più fini; nella prima i segni t sono scelti in corrispondenza di numeri irrazionali, nella seconda di numeri razionali. Le somme di Riemann sulle partizioni di queste due successioni convergeranno rispettivamente a zero e ad uno al tendere a zero dell'ampiezza; non potrà dunque esistere il limite (unico) che definisce l'integrale di Riemann.
(Nell'immagine, per rendere tale funzione leggibile, ai numeri razionali viene assegnato valore pari all'inverso del loro denominatore in forma ridotta, p.e. f(3/7)=1/7)
Funzione f(x) = x2, per 0≤x≤1
Proviamo ora a calcolare un integrale di Riemann a mano, seguendo la definizione (anziché usare il teorema fondamentale del calcolo e cercare l'antiderivata).
Partizioniamo il dominio [0,1] in n sottointervalli identici, e come segni ti prendiamo l'estremo sinistro di ciascun sottointervallo. La nostra somma di Riemann sarà dunque:
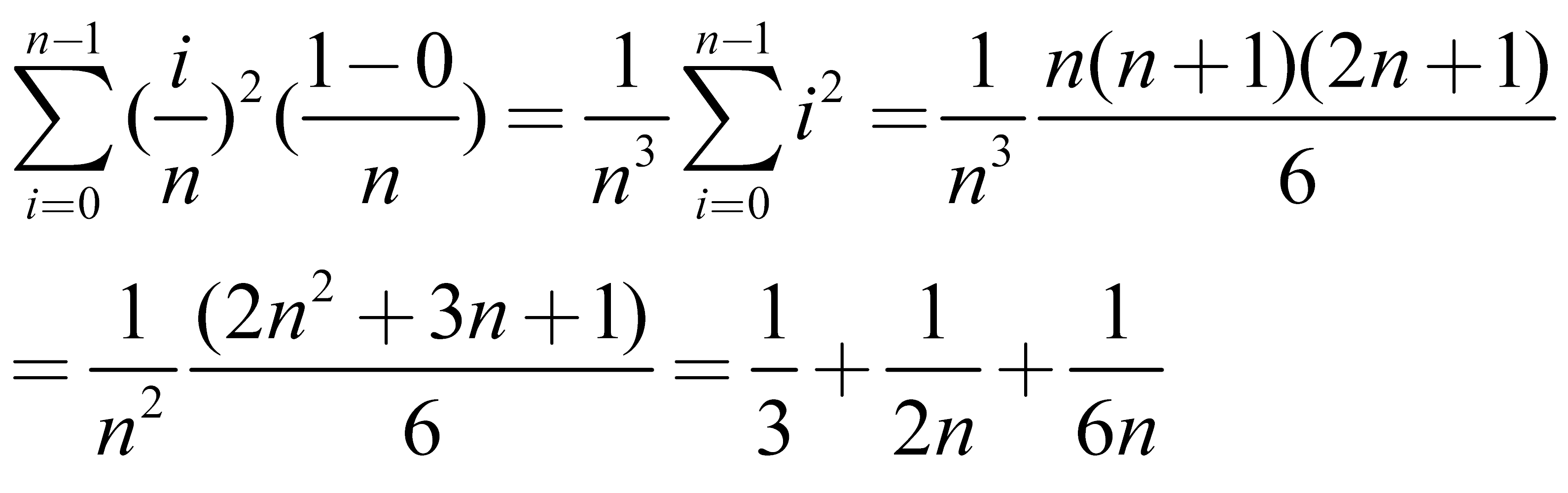
e, trattandosi di una partizione ad intervalli regolari, per mandare δ al limite infinitesimo ci è sufficiente mandare n all'infinito, ottenendo così la nostra risposta: 1/3.