Allora un sistema di equazioni cartesiane per
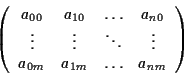
e si pongono uguali a zero gli ![]() minori orlati di
minori orlati di
![]() di ordine
di ordine ![]() nella matrice
nella matrice
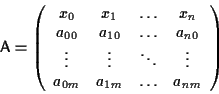
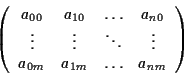
e si pongono uguali a zero gli ![]() minori orlati di
minori orlati di
![]() di ordine
di ordine ![]() nella matrice
nella matrice
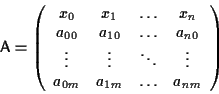
Dimostrazione
Dall'osservazione 18 della sezione ''Sottospazi proiettivi'' segue che
![]() dove
dove
![]() per ogni
per ogni
![]() Sia dunque
Sia dunque
![]()
Il vettore
![]() se e solo se
se e solo se
![]() è combinazione lineare di
è combinazione lineare di
![]() quindi se e solo se
quindi se e solo se
![]() Ma secondo il principio dei minori orlati
Ma secondo il principio dei minori orlati
![]() se e solo se tutti i minori orlati di una sottomatrice quadrata di ordine
se e solo se tutti i minori orlati di una sottomatrice quadrata di ordine ![]() e di rango
e di rango ![]() sono nulli.
sono nulli.
Notiamo che si può sicuramente trovare una sottomatrice quadrata di ordine ![]() e di rango
e di rango ![]() in quanto i vettori
in quanto i vettori
![]() sono linearmente indipendenti
sono linearmente indipendenti ![]() per l'indipendenza lineare dei punti
per l'indipendenza lineare dei punti
![]() Senza ledere la generalità possiamo supporre che sia per esempio la sottomatrice
Senza ledere la generalità possiamo supporre che sia per esempio la sottomatrice
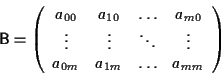
Allora
![]() se e solo se
se e solo se
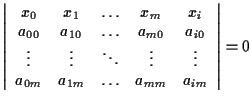 per ogni
per ogni
![]()
Abbiamo quindi ![]() equazioni cartesiane che rappresentano
equazioni cartesiane che rappresentano
![]()
![]() e che quindi, per la definizione 4, rappresentano
e che quindi, per la definizione 4, rappresentano ![]() corrispondenti agli
corrispondenti agli ![]() modi di orlare la sottomatrice
modi di orlare la sottomatrice
![]()

|
 |
 |
 |