Si consideri
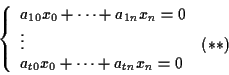
cioè dall'uguaglianza
![]() dove
dove
![]() è la matrice
è la matrice
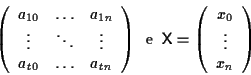
![]() vale a dire:
vale a dire:
![]()
Allora l'insieme dei punti
![]() le cui coordinate
omogenee sono soluzioni di tutte le equazioni del sistema
le cui coordinate
omogenee sono soluzioni di tutte le equazioni del sistema
![]() è
è
![]()
Infatti il punto
![]() se e solo se (osservazione 4 della sezione ''Sottospazi proiettivi'')
se e solo se (osservazione 4 della sezione ''Sottospazi proiettivi'')
![]() ovvero se e solo se
ovvero se e solo se
![]() cosa che vale se e solo se per ogni
cosa che vale se e solo se per ogni
![]() cioè se e solo se le coordinate omogenee di
cioè se e solo se le coordinate omogenee di
![]() soddisfano il sistema di equazioni omogenee
soddisfano il sistema di equazioni omogenee
![]()
Le
![]() si dicono pertanto
equazioni cartesiane del sottospazio proiettivo
si dicono pertanto
equazioni cartesiane del sottospazio proiettivo
![]() nel riferimento
nel riferimento
![]()



