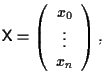 come nella definizione 4.
Sia
come nella definizione 4.
Sia Allora esistono equazioni cartesiane per
Quindi il numero minimo di equazioni cartesiane necessarie per descrivere il sottospazio proiettivo
Viceversa, se
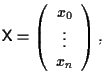 come nella definizione 4.
Sia
come nella definizione 4.
Sia
Dimostrazione
Sia
![]() con
con
![]() sottospazio vettoriale di
sottospazio vettoriale di
![]() Allora esistono equazioni cartesiane per
Allora esistono equazioni cartesiane per ![]() essendo
questo vero per ogni
essendo
questo vero per ogni
![]() sottospazio vettoriale di
sottospazio vettoriale di
![]() Inoltre vale:
Inoltre vale:
![]()

|
 |
 |
 |