esempi

6 ESEMPIO In $\mathbf{P^2(R)}$

considerato col riferimento proiettivo standard $\mathcal{S})$ l'equazione

determina una retta

Si può quindi scrivere

quindi $s=\{ [t_0,t_1,t_0+t_1]:t_0,t_1 \in \mathbf{R},(t_0,t_1) \neq (0,0) \}.$ Da notare che

è una retta anche se ha due parametri. Tali parametri sono omogenei, infatti valori proporzionali di questi danno lo stesso punto della retta (per esempio:

danno lo stesso punto).
Per decidere se un punto $Q \in \mathbf{P(V)}$ appartiene ad

basta vedere se l'equazione è risolta per un rappresentante qualsiasi di

Per esempio, vediamo se

appartiene ad

$1-1-3=-3 \neq 0,$ quindi $Q \not \in s.$

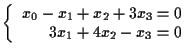7 ESEMPIO In $\mathbf{P^3(R)}$ il sistema $\left\{ \begin{array}{c} x_0 -x_1 +x_2 +3x_3 =0\\ \; \; \; \; \; \; 3x_1 +4x_2 -x_3 =0 \end{array} \right.$ definisce una retta. Infatti 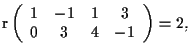$\mathrm{r} \left( \begin{array}{cccc} 1 & -1 & 1 & 3\\ 0 & 3 & 4 & -1 \end{array} \right) =2,\;$ quindi $\dim S=3-2=1.$

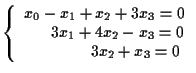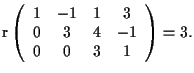
Il sistema $\left\{ \begin{array}{c} x_0 -x_1 +x_2 +3x_3 =0\\ \; \; \; \; \; \; 3x_1 +4x_2... ...\\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; 3x_2 + x_3 =0 \end{array} \right.$ determina un punto, infatti $\mathrm{r} \left( \begin{array}{cccc} 1 & -1 & 1 & 3\\ 0 & 3 & 4 & -1\\ 0 & 0 & 3 & 1 \end{array} \right) =3.$

Il sistema 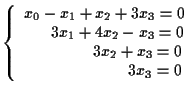$\left\{ \begin{array}{c} x_0 -x_1 +x_2 +3x_3 =0\\ \; \; \; \; \; \; 3x_1 +4x_2... ... \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; 3x_3 =0 \end{array} \right.$ rappresenta il vuoto, infatti 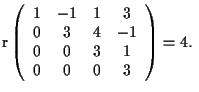$\mathrm{r} \left( \begin{array}{cccc} 1 & -1 & 1 & 3\\ 0 & 3 & 4 & -1\\ 0 & 0 & 3 & 1 \\ 0 & 0 & 0 & 3 \end{array} \right) =4.\;$ In effetti le equazioni di quest'ultimo sono 4 equazioni linearmente indipendenti in 4 incognite, quindi l'unica soluzione è ma $(0,0,0,0) \not \in \mathbf{P^3(R)},$ pertanto l'insieme delle soluzioni è vuoto.

8 ESEMPIO Consideriamo $\mathbf{P^3(R)}$ col riferimento proiettivo standard $\mathcal{S}.$ Sia

il piano di equazione

Allora

$\begin{displaymath}H \cap K= \{ [x_0, x_1, x_2, x_3] \in \mathbf{P^3(R)} : \le... ..._0 -x_1 +x_3 =0\\ 2x_0 +x_2 -3x_3 =0 \end{array} \right. \}.\end{displaymath}$

Poiché tale sistema ha rango 2, $H \cap K$ è una retta.