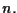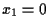
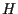
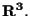
2 ESEMPIO   Consideriamo l'equazione $x_1 =0$ del piano vettoriale $H$ in $\mathbf{R^3}.$

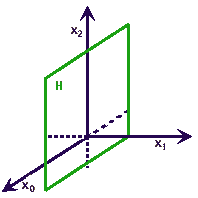
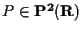
Tale equazione è omogenea, quindi ha senso cercare di capire quali punti $P \in \mathbf{P^2 (R)}$ annullano il polinomio $x_1.$
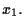
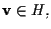
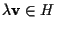
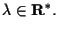
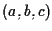
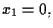
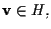
Osserviamo che se $\mathbf{v} \in H,$ allora anche $\lambda \mathbf{v} \in H$ per ogni $\lambda \in \mathbf{R^{\ast}}.$ In altri termini: se $P=[a, b, c]= [\mathbf{v}]$ è un punto tale che la terna $(a,b,c)$ soddisfa l'equazione $x_1 =0,$ allora ogni altro rappresentante del punto soddisfa tale equazione. 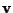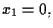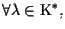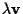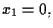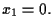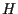Inoltre $[\mathbf{v}] \in \mathbf{P}(H)$ se e solo se $\mathbf{v} \in H,$ e ciò vale se e solo se $\mathbf{v}$ soddisfa l'equazione $x_1 =0,$ quindi se e solo se $\forall \lambda \in \mathrm{K}^{\ast},$ $\lambda \mathbf{v}$ soddisfa l'equazione $x_1 =0,$ cioè se e solo se $[ \mathbf{v} ]$ soddisfa l'equazione $x_1 =0.$ Pertanto anche la retta proiettiva associata ad $H$ è individuata dall'equazione $x_1 =0.$
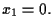
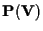
Tale discorso può essere facilmente generalizzato ad uno spazio proiettivo $\mathbf{P(V)}$ di dimensione $n.$

PAGINA PRECEDENTE INIZIO PAGINA PAGINA SUCCESSIVA