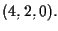1 OSSERVAZIONE
Consideriamo lo spazio proiettivo
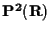
col riferimento canonico
e il punto
![$P=[2,1,3] \in \mathbf{P^2 (R)}.$](img4.gif)
Si vede subito che non ha alcun senso chiedersi se un polinomio non omogeneo,
come per esempio il polinomio
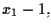
si annulli in
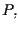
perché
![$P=[2,1,3]=[2\lambda ,\lambda, 3 \lambda]$](img7.gif)
per ogni
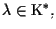
e per il rappresentante
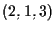
di
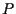
vale
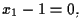
mentre per
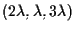
con
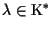
e
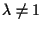
tale polinomio non si annulla. Questo accade ogni volta che
abbiamo a che fare con un polinomio lineare non omogeneo.
Sia ora
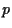
un polinomio lineare omogeneo. Allora
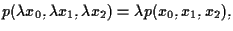
quindi se
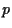
si annulla su un
rappresentante di un punto
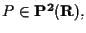
si annulla su tutti.
Pertanto in questo caso ha senso chiedersi se
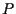
è uno zero di
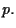
Ma
continua a non avere senso calcolare il valore di
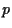
su un punto
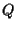
le cui
coordinate non lo annullino.
Infatti un polinomio omogeneo
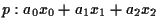
non può essere associato a una
funzione su
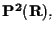
altrimenti il valore assunto dal polinomio in un
punto
![$P=[x_0,x_1,x_2]$](img22.gif)
non dipenderebbe dal rappresentante della classe di
equivalenza
![$[x_0,x_1,x_2]_{\sim}.$](img23.gif)
Per esempio: il polinomio
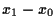
assume in
![$Q=[2,1,0]$](img25.gif)
i valori
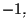
se consideriamo come rappresentante
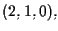
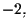
se consideriamo come rappresentante