definizione di sottospazio proiettivo

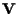
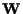
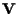
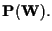
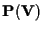
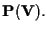
1 DEFINIZIONE Sia $\mathbf{V}$ uno spazio vettoriale. Un sottospazio vettoriale $\mathbf{W}$ di $\mathbf{V}$ ha anch'esso una struttura di spazio vettoriale, quindi ha senso considerare il suo proiettivizzato $\mathbf{P(W)}.$ Tale spazio proiettivo, contenuto in $\mathbf{P(V)}$ , è detto sottospazio proiettivo (o sottospazio lineare) di $\mathbf{P(V)}.$
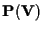
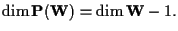
In particolare $\mathbf{P(V)}$ stesso è un sottospazio proiettivo (improprio) di se stesso. Si ha: $\dim \mathbf{P(W)} = \dim \mathbf{W} - 1.$
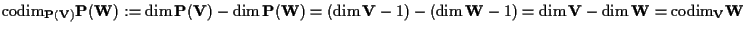
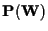
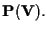
Il numero $\mathrm{codim} _{\mathbf{P(V)}} \mathbf{P(W)} : = \dim \mathbf{P(V)} - \dim \m... ... = \dim \mathbf{V} - \dim \mathbf{W} = \mathrm{codim} _{\mathbf{V}} \mathbf{W}$ è detto codimensione di $\mathbf{P(W)}$ in $\mathbf{P(V)}.$

3 DEFINIZIONE I sottospazi proiettivi di dimensione 0 sono detti punti.
I sottospazi proiettivi di dimensione 1 sono detti rette.
I sottospazi proiettivi di dimensione 2 sono detti piani.
I sottospazi proiettivi di codimensione 1 sono detti iperpiani.
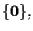
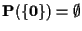
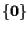
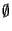
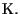
Inoltre, se consideriamo il sottospazio vettoriale banale $\{ \mathbf{0} \},$ il suo proiettivizzato è $\mathbf{P(\{ 0 \} )} = \emptyset$ (non ci sono infatti sottospazi vettoriali di dimensione 1 in $\{ \mathbf{0} \}$ ); $\emptyset$ è quindi l'unico sottospazio proiettivo di dimensione -1 di ogni spazio proiettivo su $\mathrm{K}.$

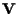
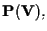
4 OSSERVAZIONE Abbiamo una corrispondenza biunivoca fra sottospazi vettoriali di $\mathbf{V}$ e sottospazi proiettivi di $\mathbf{P(V)},$ e precisamente:

$\begin{displaymath}\begin{array}{cccc} f : & \{ \mbox{sottospazi vettoriali di \... ...\}\\ \; & \mathbf{W} & \longmapsto & \mathbf{P(W)} \end{array}\end{displaymath}$

è un'applicazione iniettiva e suriettiva.
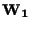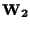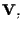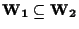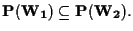
Osserviamo che tale applicazione conserva le inclusioni, cioè, dati due sottospazi vettoriali $\mathbf{W_1}$ e $\mathbf{W_2}$ di $\mathbf{V},$ allora $\mathbf{W_1} \subseteq \mathbf{W_2}$ se e solo se $\mathbf{P(W_1)} \subseteq \mathbf{P(W_2)}.$