caratterizzazione di dipendenza lineare

18 OSSERVAZIONE Dati $P_1, \ldots, P_t \in \mathbf{P(V)},$ con $P_i = [\mathbf{v_i} ]$ per $i = 1, \ldots, t,$ allora $\dim L(P_1, \ldots, P_t) \leq t - 1.$
Infatti $L(P_1, \ldots, P_t) =(\mbox{esempio 17}) \mathbf{P(<v_1, \ldots, v_t>)},$ e la dimensione del sottospazio vettoriale $\mathbf{<v_1, \ldots, v_t>}$ non supera

19 OSSERVAZIONE Possiamo dare una caratterizzazione di dipendenza (indipendenza) lineare di

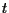
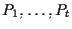
punti $P_1,\ldots,P_t$

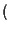
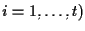
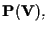
con $P_i = [\mathbf{v_i} ]$ per $i=1,\ldots,t)$ in $\mathbf{P(V)},$ in termini di dimensione del sottospazio generato da questi.
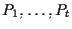
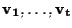
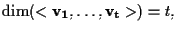
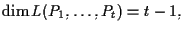
Infatti, secondo la definizione 8 della sezione ''Riferimenti proiettivi'', $P_1,\ldots,P_t$ sono linearmente indipendenti se e solo se $\mathbf{v_1}, \ldots, \mathbf{v_t}$ sono linearmente indipendenti, cioè se e solo se $\dim (\mathbf{<v_1, \ldots, v_t>}) = t,$ cioè se e solo se $\dim L(P_1, \ldots, P_t) = t - 1,$ altrimenti sono linearmente dipendenti.