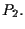17 ESEMPIO
Se
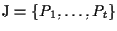
consiste di un numero finito di punti,
scriveremo
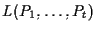
oppure
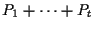
anziché
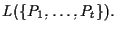
Diremo che
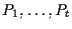 generano
generano
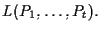
Inoltre, se
![$P_i = [\mathbf{v_i} ],$](img14.gif)
allora (per l'
osservazione 13)
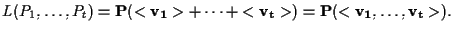
Per esempio, siano
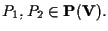
Allora il sottospazio
proiettivo
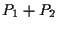
può essere di due tipi:
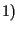
Se
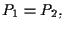
allora
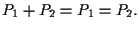
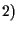
Se
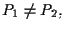
allora
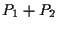
è un sottospazio di dimensione uno,
ed è l'
unica retta che contiene
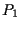
e