25 ESEMPIO
Consideriamo
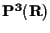
col riferimento proiettivo standard. Siano
![$P=[1,-1,3,2],Q=[0,0,1,2] \in \mathbf{P^3(R)}.$](img3.gif)
I punti
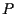
e
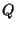
sono linearmente indipendenti, in quanto
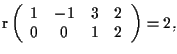
quindi
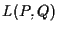
è una retta, di equazioni parametriche
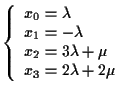
con
![$[\lambda,\mu] \in \mathbf{P^1(R)}.$](img9.gif)
Per trovare equazioni cartesiane, poi, bisogna imporre (vedi
proposizione 12)
Siccome
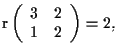
questo è equivalente a
cioè a
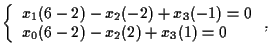
quindi
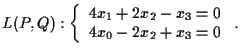
Le due equazioni del sistema sono le equazioni di due piani in
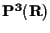
distinti, che si incontrano esattamente nella retta
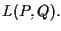
Consideriamo ora il punto
![$T=[0,-1,4,4] \not\in L(P,Q).$](img16.gif)
I tre punti
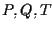
sono quindi non allineati in
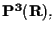
pertanto generano un piano
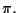
Tale piano
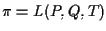
ha equazione cartesiana (vedi
esempio 14)
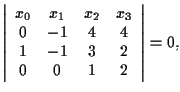
cioè
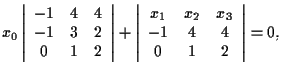
ovvero
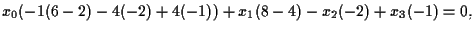
cioè
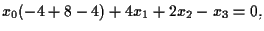
cioè
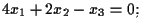
questa è un'equazione cartesiana per
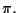
Equazioni parametriche per
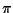
sono
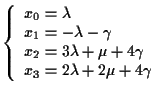
con
![$[\lambda,\mu,\gamma] \in \mathbf{P^2(R)}.$](img28.gif)
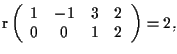 quindi
quindi 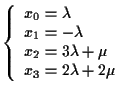 con
con
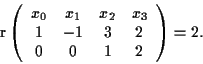
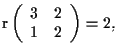 questo è equivalente a
questo è equivalente a
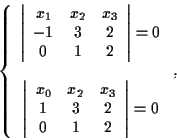
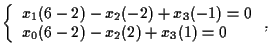 quindi
quindi
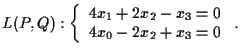 Le due equazioni del sistema sono le equazioni di due piani in
Le due equazioni del sistema sono le equazioni di due piani in
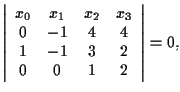 cioè
cioè
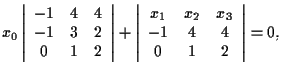 ovvero
ovvero
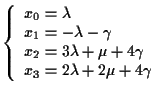 con
con


