26 ESERCIZIO
Nello spazio proiettivo reale
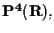
rispetto ad un riferimento proiettivo
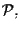
siano dati i punti:
![$A_1=[0,1,-1,1,-1], \; A_2=[1,2,-1,0,1], \; A_3=[1,0,2,1,3]$](img4.gif)
![$B_1=[1,1,0,-1,2], \; B_2=[1,3,0,7,0], \; B_3=[1,2,-1,0,3].$](img5.gif)
Verificare che i punti di ciascuna terna
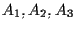
e
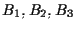
sono linearmente indipendenti e trovare le equazioni parametriche e cartesiane per i piani proiettivi
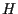
ed
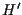
determinati da ciascuna terna.

Determinare l'intersezione

27 ESERCIZIO
Determinare le coordinate proiettive omogenee del punto di intersezione della
retta
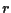
passante per i due punti distinti
![$[1,0,1,0,1]$](img3a.gif)
e
![$[2,-1,2,-1,2]$](img4a.gif)
dello spazio proiettivo

con l'iperpiano proiettivo

individuato dai quattro punti linearmente indipendenti
![$[1,0,0,0,0],$](img7a.gif)
![$[0,1,2,3,4],$](img8a.gif)
![$[0,2,1,2,0],$](img9a.gif)
e
![$[0,2,2,0,1].$](img10a.gif)





