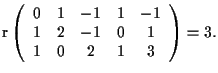 Si ha:
Si ha:
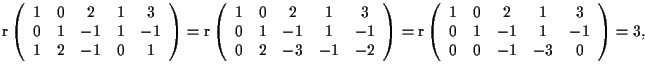 quindi
quindi
I punti
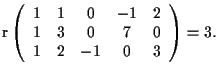 Si ha:
Si ha:
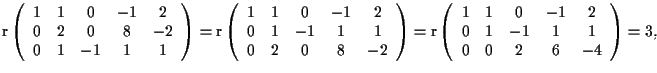 quindi
quindi
Una rappresentazione parametrica omogenea dei due piani è:
Soluzione
![]() I punti
I punti
![]() sono linearmente indipendenti se e solo se
sono linearmente indipendenti se e solo se
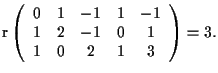 Si ha:
Si ha:
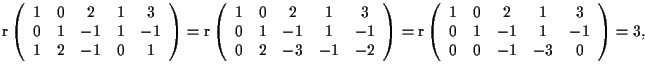 quindi
quindi
![]() sono linearmente indipendenti.
sono linearmente indipendenti.
I punti
![]() sono linearmente indipendenti se e solo se
sono linearmente indipendenti se e solo se
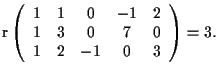 Si ha:
Si ha:
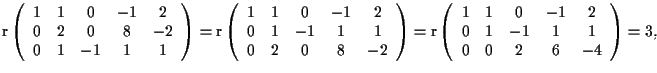 quindi
quindi
![]() sono linearmente indipendenti.
sono linearmente indipendenti.
Una rappresentazione parametrica omogenea dei due piani è:
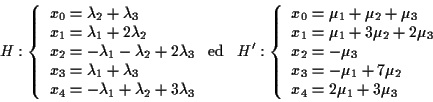
con
![]() parametri omogenei.
parametri omogenei.
Per trovare le equazioni cartesiane per i piani proiettivi ![]() ed
ed ![]() bisogna porre rispettivamente
bisogna porre rispettivamente
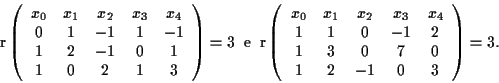
Siccome
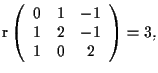 la prima condizione è verificata se e solo se
la prima condizione è verificata se e solo se
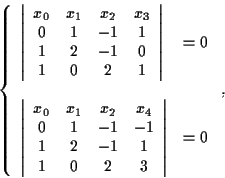
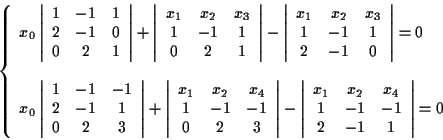
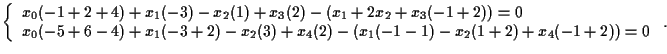 Quindi equazioni cartesiane per
Quindi equazioni cartesiane per 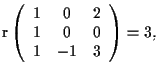 la seconda condizione è verificata se e solo se
la seconda condizione è verificata se e solo se
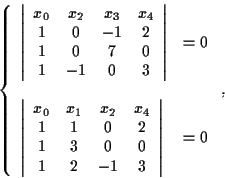
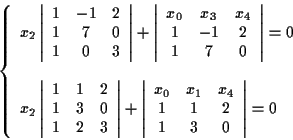
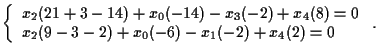 Quindi equazioni cartesiane per
Quindi equazioni cartesiane per ![$H \cap H' = \{ P=[x_0,x_1,x_2,x_3,x_4] \in \mathbf{P^4(R)}: \; (\ast)
\left\{ \...
..._0 -5x_2 -x_3 -4x_4 =0 \\
3x_0 -x_1 -2x_2 -x_4 =0 \\
\end{array} \right. \} .$](img30.gif)
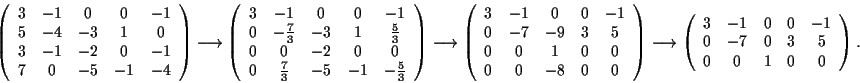
![\begin{displaymath}H \cap H'= \{ P=[x_0,x_1,x_2,x_3,x_4] \in \mathbf{P^4(R)}:
\l...
...4 =0 \\
-7x_1 +3x_3 +5x_4 =0 \\
x_2 =0
\end{array} \right. \}\end{displaymath}](img33.gif)