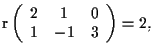esempio

24 ESEMPIO Consideriamo $\mathbf{P^2(R)}$ col riferimento proiettivo standard. Siano $P=[2,1,0],Q=[1,-1,3] \in \mathbf{P^2(R)}.$ Poiché $\mathrm{r} \left( \begin{array}{ccc} 2 & 1 & 0 \\ 1 & -1 & 3 \end{array} \right) =2,$ cioè $P \neq Q,$

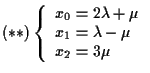è una retta che avrà equazioni parametriche $(\ast \ast) \left\{ \begin{array}{l} x_0=2\lambda +\mu \\ x_1=\lambda -\mu \\ x_2=3\mu \end{array} \right.$ con $(\lambda,\mu) \neq (0,0)$ parametri omogenei.
Vediamo su un esempio che $(\lambda,\mu)$ sono effettivamente omogenei. Se scegliamo $(\lambda,\mu)=(1,1),$ otteniamo il punto

Per $(\lambda,\mu)=(2,2),$ otteniamo ancora

Inoltre osserviamo che $r=\mathbf{P(H)},$ dove $\mathbf{H}$ è un piano in $\mathbf{R^3}$ di equazioni parametriche $(\ast \ast),$ ma con $(\lambda,\mu) \in \mathbf{R^2}.$
Consideriamo ora l'applicazione

$\begin{displaymath}\begin{array}{cccl} \varphi : & \mathbf{R^2} & \longrightarro... ...& \longmapsto & (2\lambda +\mu, \lambda -\mu ,3\mu) \end{array}\end{displaymath}$

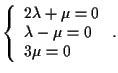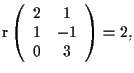Si nota subito che $\varphi$ è iniettiva, infatti $(2\lambda +\mu, \lambda -\mu ,3\mu)=(0,0,0)$ se e solo se $\left\{ \begin{array}{l} 2\lambda +\mu =0 \\ \lambda -\mu =0 \\ 3\mu =0 \end{array} \right. .$ Poiché $\mathrm{r} \left( \begin{array}{cc} 2 & 1 \\ 1 & -1 \\ 0 & 3 \end{array} \right) =2,$ le equazioni del sistema sono soddisfatte se e solo se $\lambda = \mu =0.$ Inoltre $\mathrm{Im} (\varphi) = \mathbf{H}.$
Quindi $\varphi$ è un isomorfismo tra $\mathbf{R^2}$ ed $\mathbf{H}.$
Questo accade ogni volta che si parametrizza un sottospazio vettoriale utilizzando una base. La stessa cosa vale pertanto per i sottospazi proiettivi, cioè, in questo caso particolare, esiste un isomorfismo $\Phi$ tra e $\mathbf{P^1(R)}$ (vedi la definizione-proposizione 3 della sezione "Morfismi proiettivi").
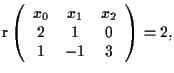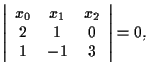Troviamo ora un'equazione cartesiana di in $\mathbf{P^2(R)}.$ Il punto appartiene alla retta se e solo se $\mathrm{r} \left( \begin{array}{ccc} x_0 & x_1 & x_2 \\ 2 & 1 & 0 \\ 1 & -1 & 3 \end{array} \right) =2,$ cioè se e solo se $\left\vert \begin{array}{ccc} x_0 & x_1 & x_2 \\ 2 & 1 & 0 \\ 1 & -1 & 3 \end{array} \right\vert =0,$ cioè se e solo se cioè