23 OSSERVAZIONE-DEFINIZIONE
Equazioni parametriche di un sottospazio proiettivo
Poiché ogni sottospazio vettoriale di
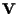
possiede una base, ogni
sottospazio proiettivo
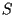
di
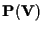
può essere generato da un numero
finito, pari a
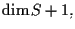
di suoi punti linearmente indipendenti.
Supponiamo per esempio che
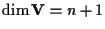
e che
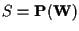
con
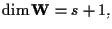
e
consideriamo una base
di
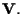
Sia inoltre
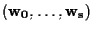
una base di
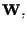
con
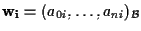
per
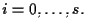
Allora abbiamo un sistema di
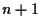
equazioni parametriche del sottospazio
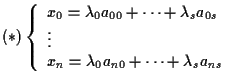
con
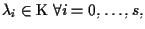
e

Infatti,
dato
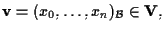
allora
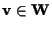
se e solo se esistono
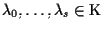
tali che
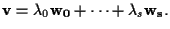
Osserviamo che le equazioni
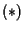
si possono pensare come equazioni
parametriche di
infatti
![$S=\mathbf{P(W)}=\{ [\mathbf{v}]:\mathbf{v} \in
\mathbf{W \backslash \{0\}} \},$](img26.gif)
cioè, posto
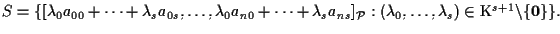
Si noti che
![$S=L([\mathbf{w_0}],\ldots,[\mathbf{w_s}])$](img29.gif)
(
esempio 17 della sezione "Sottospazi proiettivi").
Si osservi poi che le
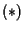
dipendono dalla scelta degli
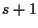
punti
![$[\mathbf{w_0}],\ldots,[\mathbf{w_s}]$](img31.gif)
di
e dalla scelta dei rappresentanti
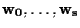
di tali punti.
Inoltre, se attribuiamo a
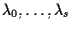
i valori della
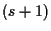
-pla
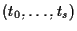
e della
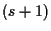
-pla
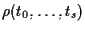
con
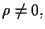
otteniamo lo stesso punto. In piú bisogna assumere
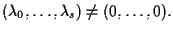
Pertanto
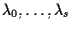
sono detti
parametri omogenei, e si può scrivere
![$S=\{ [\lambda_0
a_{00}+\cdots + \lambda_s a_{0s}, \ldots, \lambda_0 a_{n0}+\cd...
...{\mathcal{P}} : [\lambda_0,\ldots,\lambda_s] \in \mathbf{P^s}
(\mathrm{K}) \}.$](img39.gif)
Quindi:
per un sottospazio proiettivo di dimensione
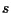
si possono trovare equazioni
parametriche dipendenti da
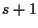
parametri omogenei
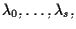
utilizzando
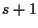
punti linearmente indipendenti del sottospazio (che è quindi
generato da tali punti).
Viceversa: date equazioni del tipo
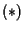
con
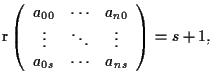
i punti
![$[a_{00},\ldots,a_{n0}]_{\mathcal{P}},\ldots,[a_{0s},\ldots,a_{ns}]_{\mathcal{P}
}$](img43.gif)
sono linearmente indipendenti e generano un sottospazio proiettivo di dimensione
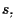
di cui le
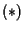
sono equazioni parametriche con
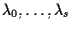
parametri omogenei.
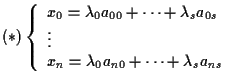 con
con

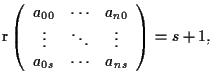 i punti
i punti



