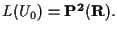esempio

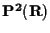
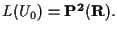
22 ESEMPIO In $\mathbf{P^2 (R)}$ $U_0 = \{ [x_0,x_1,x_2] \in \mathbf{P^2 (R)} : x_0 \neq 0 \}.$ Vediamo che $L(U_0) = \mathbf{P^2 (R)}.$
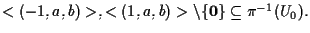
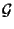
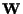
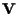
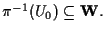
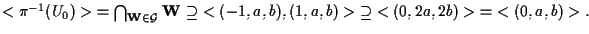
Infatti $[-1,a,b],[1,a,b] \in U_0,$ quindi (per la notazione 10 della sezione "Sottospazi proiettivi") $<(-1,a,b)>,<(1,a,b)> \backslash \{\mathbf{0}\} \subseteq \pi ^{-1} (U_0).$ Sia ora $\mathcal{G}$ la famiglia dei sottospazi vettoriali $\mathbf{W}$ di $\mathbf{V}$ tali che $\pi ^{-1} (U_0) \subseteq \mathbf{W}.$ Allora dalla relazione precedente otteniamo che $<\pi ^{-1} (U_0)>\;=\bigcap_{\small {\mathbf{W} \in \mathcal{G}}} \mathbf{W} \supseteq \; <(-1,a,b),(1,a,b)> \; \supseteq \; <(0,2a,2b)> \; =\; <(0,a,b)>.$
Quindi

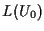
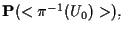
che, per osservazione 12 della sezione "Sottospazi proiettivi", è uguale a $\mathbf{P} (<\pi ^{-1} (U_0)>),$ contiene $\mathbf{P}(<(0,a,b)>)=[0,a,b] \in H_0.$
Tale ragionamento può essere fatto per ogni punto di

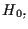
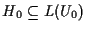
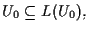
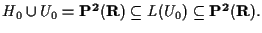
pertanto abbiamo che $H_0 \subseteq L(U_0)$ e $U_0 \subseteq L(U_0),$ quindi $H_0 \cup U_0 = \mathbf{P^2 (R)} \subseteq L(U_0) \subseteq \mathbf{P^2 (R)}.$ Dunque vale l'uguaglianza $L(U_0) = \mathbf{P^2 (R)}.$