sottospazio proiettivo generato da un sottinsieme

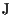
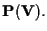
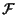
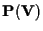
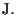
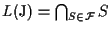
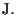
9 DEFINIZIONE Sia $\mathrm{J}$ un sottinsieme non vuoto di $\mathbf{P(V)}.$ Sia $\mathcal{F}$ la famiglia dei sottospazi proiettivi di $\mathbf{P(V)}$ che contengono $\mathrm{J}.$ Allora $L(\mathrm{J}) = \bigcap_{ \small {S \in \mathcal{F}}} S$ si dice sottospazio proiettivo generato da $\mathrm{J}.$
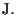
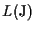
Questo è il piú piccolo sottospazio proiettivo che contiene $\mathrm{J}.$ Infatti $L(\mathrm{J})$ è un sottospazio proiettivo per la proposizione 7, e se

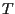
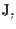
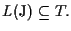
è un sottospazio proiettivo che contiene $\mathrm{J},$ allora $L(\mathrm{J}) \subseteq T.$
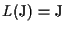
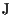
Ovviamente $L(\mathrm{J}) = \mathrm{J}$ se e solo se $\mathrm{J}$ è un sottospazio proiettivo .

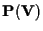
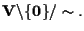
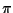
10 NOTAZIONE Abbiamo visto nell'osservazione 3 della sezione ``Definizione di sottospazio proiettivo'' che c'è una corrispondenza biunivoca tra $\mathbf{P(V)}$ e $\mathbf{V \backslash \{0\}} / \sim.$ D'ora in poi denoteremo con $\pi$ la proiezione naturale

$\begin{displaymath}\begin{array}{cccccc} \pi : & \mathbf{V \backslash \{0\}} & ... ...ngmapsto & [\mathbf{v} ] & = & [\mathbf{v} ]_{\sim} \end{array}\end{displaymath}$

La controimmagine di $[\mathbf{v} ]$ sarà $\pi^{-1} \{ [\mathbf{v} ] \} = <\mathbf{v} >\backslash \{ \mathbf{0}\} = \{ \lambda \mathbf{v} : \lambda \neq 0 \}.$

11 OSSERVAZIONE Sia $\mathrm{J} \neq \emptyset$ un sottinsieme qualsiasi di $\mathbf{P(V)}.$ Sia $\mathbf{W}$ un sottospazio vettoriale di $\mathbf{V}.$ Allora risulta: $\mathrm{J} \subseteq \mathbf{P(W)}$ se e solo se $\pi^{-1} (\mathrm{J}) \subseteq \mathbf{W}.$

Infatti:
$\Rightarrow \; )$ Se $\mathrm{J} \subseteq \mathbf{P(W)},$ allora $\pi^{-1} (\mathrm{J}) \subseteq \pi^{-1} (\mathbf{P(W)}) = \mathbf{W} \backslash \{\mathbf{0}\} \subseteq \mathbf{W}.$
$\Leftarrow \; )$ Sia $\pi^{-1} (\mathrm{J}) \subseteq \mathbf{W};$ allora vale, dato che $\mathbf{0} \not \in \pi^{-1} (\mathrm{J}),$ $\pi^{-1} (\mathrm{J}) \subseteq \mathbf{W} \backslash \{\mathbf{0}\},$ e quindi $\pi (\pi^{-1} (\mathrm{J})) = \mathrm{J} \subseteq \pi (\mathbf{W} \backslash \{\mathbf{0}\}) = \mathbf{P(W)}.$