1 DEFINIZIONE
Nel seguito
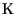
denoterà sempre un campo fissato e
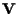
un
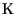
-spazio vettoriale di dimensione
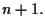
Lo
spazio proiettivo su
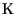
associato a
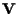
è l'insieme
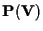
i cui elementi, chiamati
punti di
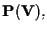
sono i sottospazi vettoriali di dimensione uno di
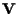
,
cioè le rette vettoriali di
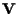
;
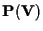
è anche chiamato
proiettivizzazione (o
proiettivizzato) di
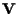
.
2 OSSERVAZIONE
Ogni
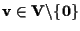
genera il sottospazio di
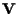
di dimensione uno
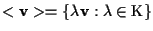
.
Quando lo considereremo come un punto di
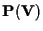
,
denoteremo questo sottospazio col simbolo
![$[\mathbf{v} ]$](img8.gif)
.
Si nota subito che due vettori
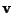
,
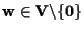
definiscono lo stesso punto di
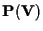
,
cioè
![$[\mathbf{v}]=[\mathbf{w}]$](img11.gif)
se e solo se esiste
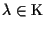
,
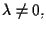
tale che
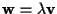
.
3 OSSERVAZIONE
C'è una corrispondenza biunivoca naturale tra
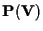
e l'insieme quoziente
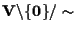
,
dove
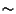
è la relazione di equivalenza seguente:
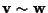
se e solo se esiste
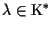
tale che
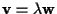
,
cioè:
Possiamo allora identificare
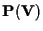 con
con
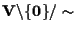 ,
scrivendo
,
scrivendo
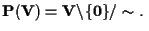 È per questo motivo che i punti di
È per questo motivo che i punti di
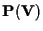 sono indicati, solitamente, racchiudendo un elemento di
sono indicati, solitamente, racchiudendo un elemento di
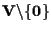 fra parentesi quadre:
fra parentesi quadre:
![$[\;\cdot\;]$](img23.gif) .
Tale scrittura indica una classe di equivalenza, e il puntino fra parentesi quadre un suo rappresentante.
.
Tale scrittura indica una classe di equivalenza, e il puntino fra parentesi quadre un suo rappresentante.
4 PROPOSIZIONE
La relazione
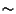
definita in
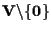
è una relazione di equivalenza.
Dimostrazione
Vale l'uguaglianza
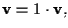 quindi
quindi 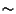 è riflessiva.
è riflessiva.
Se
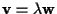 ,
allora
,
allora
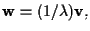 quindi
quindi 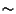 è simmetrica.
è simmetrica.
Se
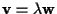 e
e
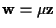 ,
allora
,
allora
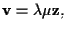 quindi
quindi 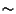 è transitiva.
è transitiva.
![]() con
con
![]() ,
scrivendo
,
scrivendo
![]() È per questo motivo che i punti di
È per questo motivo che i punti di
![]() sono indicati, solitamente, racchiudendo un elemento di
sono indicati, solitamente, racchiudendo un elemento di
![]() fra parentesi quadre:
fra parentesi quadre:
![]() .
Tale scrittura indica una classe di equivalenza, e il puntino fra parentesi quadre un suo rappresentante.
.
Tale scrittura indica una classe di equivalenza, e il puntino fra parentesi quadre un suo rappresentante. ![]() quindi
quindi ![]() è riflessiva.
è riflessiva.
![]() ,
allora
,
allora
![]() quindi
quindi ![]() è simmetrica.
è simmetrica.
![]() e
e
![]() ,
allora
,
allora
![]() quindi
quindi ![]() è transitiva.
è transitiva.



