Basi ortonormali

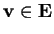
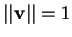
Definizione 3.1   Un vettore $\mathbf{v} \in \mathbf{E}$ è detto versore se $\vert\vert\mathbf{v}\vert\vert=1$.
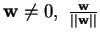
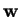
Se $\mathbf{w} \neq 0, \, \, \frac{\mathbf{w}}{\vert\vert\mathbf{w}\vert\vert}$ è un versore parallelo a $ \mathbf{w}$ e si dice che si ottiene normalizzando $ \mathbf{w}$.
Un insieme finito di vettori non nulli è detto insieme ortogonale di vettori se
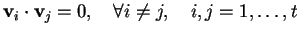
$\mathbf{v}_{i} \cdot \mathbf{v}_{j}=0, \quad \forall i \neq j, \quad i,j=1,\ldots,t$.
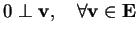
Da notare che $0 \perp \mathbf{v}, \quad \forall \mathbf{v} \in \mathbf{E}$ e, poichè il prodotto scalare è definito positivo, è l'unico vettore con questa caratteristica.
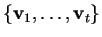
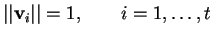
L'insieme $\lbrace \mathbf{v}_{1},\ldots,\mathbf{v}_{t} \rbrace $ è detto ortonormale se soddisfa l' ortogonalità e se inoltre i vettori hanno tutti norma unitaria, cioè $\vert\vert\mathbf{v}_{i}\vert\vert=1, \qquad i=1,\ldots,t$.
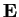
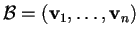
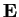
Analoghe definizioni si danno per una base di $\mathbf{E}$: in particolare, preso un prodotto scalare standard, allora una base $\mathcal{B}=(\mathbf{v}_{1},\ldots,\mathbf{v}_{n})$ per $\mathbf{E}$ è detta ortonormale se soddisfa:

\begin{displaymath}f(\mathbf{v}_{i},\mathbf{v}_{j})= \mathbf{v}_{i} \cdot \mathb... ...n{array}{ll} 0 & i \neq j\\ 1 & i=j \end{array} \right. , \end{displaymath}

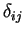
( $\delta_{ij}$ che si chiama simbolo di Kronecker).
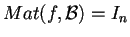
Si avrà quindi $Mat(f,\mathcal{B})=I_{n}$, matrice identità.

Proposizione 3.2   Sia $\lbrace \mathbf{v}_{1},\ldots,\mathbf{v}_{t} \rbrace $ un insieme ortogonale di vettori; allora
1.
$\lbrace \frac{\mathbf{v}_{1}}{\vert\vert\mathbf{v}_{1}\vert\vert},\ldots,\frac{\mathbf{v}_{t}}{\vert\vert\mathbf{v}_{t}\vert\vert} \rbrace$ è un insieme ortonormale.
(Si dirà che abbiamo normalizzato i vettori.)
2.
$\mathbf{v}_{1},\ldots,\mathbf{v}_{t}$ sono linearmente indipendenti.

Dimostrazione

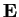
Proposizione 3.3   Esistono sempre basi ortonormali per $\mathbf{E}$.
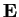
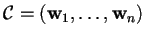
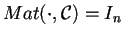
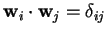
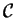
Infatti il prodotto scalare che è dato su $\mathbf{E}$ è una particolare forma bilineare simmetrica definita positiva, quindi per il teorema di Sylvester esiste una base $\mathcal{C}=(\mathbf{w}_{1},\ldots,\mathbf{w}_{n})$ tale che $Mat(\cdot,\mathcal{C})=I_{n}$, cioè $\mathbf{w}_{i} \cdot \mathbf{w}_{j}= \delta_{ij}$, quindi $\mathcal{C}$ è una base ortonormale.

Per costruire una base ortonormale $\mathcal{C}$ utilizziamo le tecniche già viste:
consideriamo un vettore $\mathbf{v}_{1} \neq 0; \mathbf{v}_{1}$ non è isotropo perché $\mathbf{v}_{1} \cdot \mathbf{v}_{1}>0, \,\, \forall \mathbf{v} \neq 0$,
quindi
$\mathbf{E}=<\mathbf{v}_{1}> \oplus \, \mathbf{v}_{1}^{\perp}$.
In $\mathbf{v}_{1}^{\perp}$ un qualsialsi vettore $\mathbf{v}_{2} \neq 0 $ è non isotropo, quindi:
$\mathbf{E}=<\mathbf{v}_{1}> \oplus \, <\mathbf{v}_{2}> \oplus \, (\mathbf{v}_{1}^{\perp} \cap \mathbf{v}_{2}^{\perp})$
e procedendo come spiegato nella dimostrazione del teorema (1.3), si ottiene:
$\mathbf{E}=<\mathbf{v}_{1}> \oplus \, <\mathbf{v}_{2}> \, \oplus \, \ldots \, \oplus \, <\mathbf{v}_{n}>$.
Infine, normalizzando, trovo la base cercata:

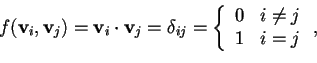
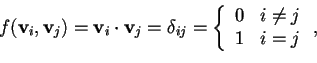
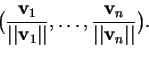
\begin{displaymath}\big( \frac{\mathbf{v}_{1}}{\vert\vert\mathbf{v}_{1}\vert\ver... ...ac{\mathbf{v}_{n}}{\vert\vert\mathbf{v}_{n}\vert\vert} \big). \end{displaymath}

Osserviamo che, se abbiamo una base ortonormale su $\mathbf{E}$, il prodotto scalare di due vettori si esprime come il prodotto scalare standard fra i vettori riga e colonna formati dalle loro coordinate rispetto a tale base.
Questo semplifica decisamente i calcoli, ed è quindi sempre conveniente utilizzare basi ortonormali:

Proposizione 3.4   Sia $\mathcal{B}=(\mathbf{v}_{1},\ldots,\mathbf{v}_{n})$ una base ortonormale; allora
$(x_{1},\ldots,x_{n})_{\mathcal{B}} \cdot (y_{1},\ldots,y_{n})_{\mathcal{B}}=x_{1}y_{1}+ \cdots+ x_{n}y_{n}, \quad $ e in particolare:

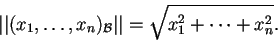
\begin{displaymath}\vert\vert(x_{1},\ldots,x_{n})_{\mathcal{B}}\vert\vert= \sqrt{x_{1}^{2}+ \cdots + x_{n}^{2}}. \end{displaymath}

Dimostrazione

Proposizione 3.5   Siano $\mathcal{B}=(\mathbf{v}_{1},\ldots,\mathbf{v}_{n})$ una base ortonormale e $\mathcal{C}=(\mathbf{w}_{1},\ldots,\mathbf{w}_{n})$ una base qualunque di $\mathbf{E}$. Allora
$\mathcal{C}$ è ortonormale      $\Longleftrightarrow \quad M_{\mathfrak{BC} }(id_{\mathbf{V}})$ è ortogonale.

Dimostrazione