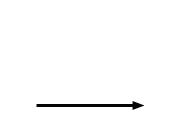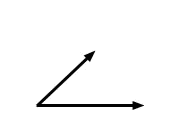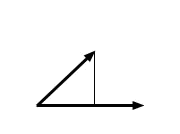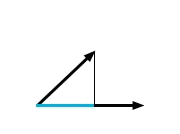
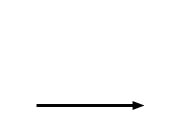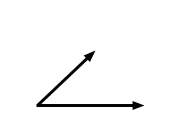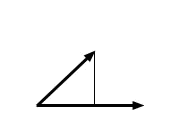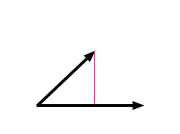
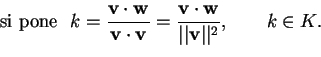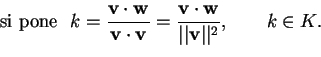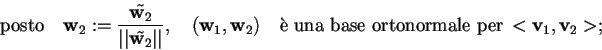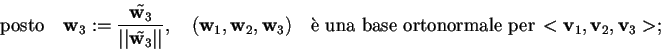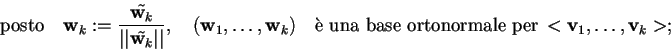Ortogonalizzazione di Gram-Schmidt

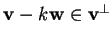
Definizione 4.1 Sappiamo che $\mathbf{v}-k\mathbf{w} \in \mathbf{v}^{\perp}$ ; allora chiameremo

	proiezione ortogonale di w nella direzione di v il vettore $k \, \mathbf{w}$ , e lo indicheremo con $p_{\mathbf{v}}(\mathbf{w})$ ,
	e diremo il vettore $\mathbf{w}-p_{\mathbf{v}}(\mathbf{w}) \, \mathbf{v}$ il perpendicolare di w a v .

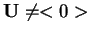
Ora cerchiamo la proiezione di un vettore su un sottospazio $\mathbf{U} \neq <0>$ :
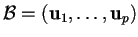
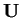
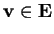
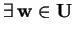
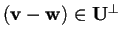
sia $\mathcal{B}=(\mathbf{u}_{1},\ldots,\mathbf{u}_{p})$ una base di $\mathbf{U}$ , consideriamo un vettore $\mathbf{v} \in \mathbf{E}$ e determiniamo se $\exists \, \mathbf{w} \in \mathbf{U}$ tale che $(\mathbf{v}-\mathbf{w}) \in \mathbf{U}^{\perp}$ .
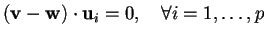
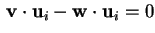
Si ha che $(\mathbf{v}-\mathbf{w})\cdot\mathbf{u}_{i}=0, \quad \forall i=1,\ldots,p \,$ se e solo se $\,\mathbf{v}\cdot\mathbf{u}_{i}-\mathbf{w}\cdot\mathbf{u}_{i}=0$ ; cioè se e solo se

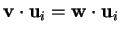
$\mathbf{v} \cdot \mathbf{u}_{i}= \mathbf{w} \cdot \mathbf{u}_{i}$ .

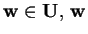
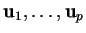
Poiché $\mathbf{w} \in \mathbf{U}, \, \mathbf{w}$ si esprime come combinazione lineare di $\mathbf{u}_{1},\ldots,\mathbf{u}_{p}$ :
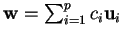
$\mathbf{w}=\sum_{i=1}^{p}c_{i}\mathbf{u}_{i}$ .
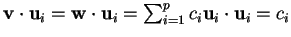
Avremo $\mathbf{v} \cdot \mathbf{u}_{i}= \mathbf{w} \cdot \mathbf{u}_{i}= \sum_{i=1}^{p}c_{i}\mathbf{u}_{i} \cdot \mathbf{u}_{i}=c_{i}$
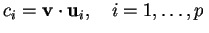
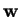
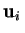
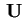
Gli scalari $c_{i}=\mathbf{v} \cdot \mathbf{u}_{i}, \quad i=1,\ldots,p \,$ sono le proiezioni ortogonali di $\mathbf{w}$ rispetto alle direzioni individuate dagli $\mathbf{u}_{i} \,$ di $\, \mathbf{U}$ .
Vediamo direttamente in cosa consiste il procedimento di Gram-Schmidt:
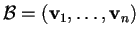
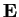
prendiamo una base $\mathcal{B}=(\mathbf{v}_{1},\ldots,\mathbf{v}_{n})$ di uno spazio euclideo $\mathbf{E}$ .
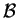
Se $\mathcal{B}$ non è ortonormale:

$\begin{displaymath}\mathbf{w}_{1}:= \frac{\mathbf{v}_{1}}{\vert\vert\mathbf{v}_{... ...tore ortonormale, e} \quad <\mathbf{w}_{1}>=<\mathbf{v}_{1}>; \end{displaymath}$

$\begin{displaymath}\tilde{\mathbf{w}_{2}}:=\mathbf{v}_{2}-(\mathbf{v}_{2} \cdot ... ...le di $\mathbf{v}_{2}$\space su} \, <\mathbf{v}_{1}>^{\perp}; \end{displaymath}$

$\begin{displaymath}\textrm{posto}\quad \mathbf{w}_{2}:= \frac{\tilde{\mathbf{w}_... ...una base ortonormale per} \, <\mathbf{v}_{1},\mathbf{v}_{2}>; \end{displaymath}$

$\begin{displaymath}\tilde{\mathbf{w}_{3}}:=\mathbf{v}_{3}-(\mathbf{v}_{3} \cdot ... ...v}_{3}$\space su} \, <\mathbf{v}_{1},\mathbf{v}_{2}>^{\perp}; \end{displaymath}$

$\begin{displaymath}\textrm{posto}\quad \mathbf{w}_{3}:= \frac{\tilde{\mathbf{w}_... ...rmale per} \, <\mathbf{v}_{1},\mathbf{v}_{2},\mathbf{v}_{3}>; \end{displaymath}$

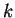
-esimo passo:

$\begin{displaymath}\tilde{\mathbf{w}_{k}}:=\mathbf{v}_{k}- \sum_{i=1}^{k-1} (\ma... ...pace su} \, <\mathbf{v}_{1},\ldots,\mathbf{v}_{k-1}>^{\perp}; \end{displaymath}$

$\begin{displaymath}\textrm{posto}\quad \mathbf{w}_{k}:= \frac{\tilde{\mathbf{w}_... ...e ortonormale per} \, <\mathbf{v}_{1},\ldots,\mathbf{v}_{k}>; \end{displaymath}$

Si procede così fino all'

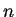
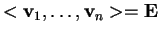
-esima iterazione, dove $<\mathbf{v}_{1},\ldots,\mathbf{v}_{n}>=\mathbf{E}$ .
In base a tale procedimento si dà il seguente teorema:

Teorema 4.2 (di ortogonalizzazione di Gram-Schmidt) Sia $\mathbf{v}_{1},\mathbf{v}_{2},\ldots,\mathbf{v}_{n}$ una successione (finita o infinita) di vettori linearmente indipendenti dello spazio euclideo $\mathbf{E}$ . Allora:

1.

Esiste una successione (rispettivamente finita dello stesso numero di elementi, o infinita) $\mathbf{w}_{1},\ldots,\mathbf{w}_{n}$ di vettori di $\mathbf{E}$ tale che $\forall k \geq 1$ , intero, si abbia:

-: $<\mathbf{v}_{1},\mathbf{v}_{2},\ldots,\mathbf{v}_{k}>=<\mathbf{w}_{1},\mathbf{w}_{2},\ldots,\mathbf{w}_{k}>$ ;
-: i vettori $\mathbf{w}_{1},\ldots,\mathbf{w}_{k}$ sono a due a due ortogonali.

2.

Se $\mathbf{u}_{1},\mathbf{u}_{2},\ldots$ è un'altra successione che soddisfa le condizioni qui sopra, $\forall k \geq 1$ intero, allora esistono scalari non nulli $c_{1},c_{2},\ldots$ tali che:

$\mathbf{u}_{k}=c_{k}\mathbf{w}_{k}, \quad \forall k \geq 1$